
Il n’y a sans doute aujourd’hui guère d’élève ou d’enseignant qui n’ait rencontré au cours de sa scolarité un encart historique relatant la mesure de la pyramide par Thalès. Tous ces encarts rapportent une scène qui se situe à peu près à l’origine de nos mathématiques au cours de laquelle Thalès applique le théorème fondamental qui porte son nom. C’est sans doute le récit historique de loin le plus connu : il est à la fois un récit de l’origine des mathématiques et exemplaire, sinon à l’origine, du rapport à l’histoire des mathématiques à l’œuvre dans les manuels scolaires.
Ces encarts vont nous donner l'occasion de découvrir les thèmes privilégiés et les principales caractéristiques de l’histoire présentée dans nos manuels de mathématiques. Nous allons rencontrer le thème de la justification d'une dénomination et celui de la recherche de l'origine. Nous verrons aussi différentes manifestations de condescendance, certaines propres à ces encarts, d'autres communes à la plupart. Nous allons enfin découvrir et voir l'importance de la circularité, des faux-amis qui lui sont associés, et de la récapitulation qui constituent, avec la condescendance, les principales caractéristiques historiographiques des encarts historiques de nos manuels de mathématiques.
Considérons un de ces encarts historiques qui présente la mesure d'une des pyramides d'Égypte par Thalès :

Cet encart historique accompagne l’introduction du théorème de Thalès en collège. La mesure de la hauteur d'une pyramide est en effet un bel exemple d'application des mathématiques. Une pyramide est un volume impénétrable, un tombeau, qu'il faudrait a priori traverser verticalement, de son sommet à sa base, pour en mesurer la hauteur. Cette mesure paraît difficile, voire impossible, à réaliser directement. Le théorème de Thalès permet de s'affranchir de cette difficulté et de réaliser une telle mesure sans violer la sépulture en utilisant simplement l'ombre projetée par un bâton dans un pays où le Soleil dispense généreusement ses rayons. La connaissance de ce théorème permet de ramener l'inaccessible à l'accessible ; elle augmente nos capacités.
Tout cela est très bien, mais pour l'instant sans rapport avec l'histoire... L’histoire intervient avec la mention de Thalès :
Lors d'un voyage en Égypte, le mathématicien et philosophe grec Thalès de Milet (VIe siècle av. J.-C) découvrit la pyramide de Khéops dont personne ne pouvait mesurer la hauteur selon le Pharaon Amasis. Thalès décida de relever le défi.
Le récit historique rapporté nous présente l'application du « théorème de Thalès » par Thalès lui-même. Étant entendu que ce théorème a dû être découvert par Thalès, nous sommes témoins d'une sorte de « scène primitive » : Thalès appliquant lui-même son théorème. Il ne s'agit plus d'un énoncé désincarné, mais de sa forme originelle : un théorème vivant, le théorème en personne. L'histoire seule peut nous offrir un spectacle aussi fascinant. Son intérêt tient sans doute pour une part à l'attrait toujours vif exercé par les récits mythologiques : le « théorème de Thalès » agit et parle dans ce récit comme les animaux ou les objets dans un mythe. Ce récit se présente comme un récit d'origine (d'un théorème) et en a le caractère mythologique. Les pharaons sont propices aux représentations d'ordre mythologique. La rencontre dans le désert, lieu privilégié pour les récits des origines, de l'un d'entre eux avec un savant grec peut elle-même sembler tout à fait irréelle tant ces deux civilisations sont sans doute disjointes dans l'esprit de nombre d'élèves.
Ainsi, cet encart nous fait assister à la rencontre de Thalès et du Pharaon et met en scène l'efficacité de la rationalité mathématique dans un récit de facture mythologique. Cette alliance du rationnel et du mythologique renforce l'impression d'assister à une scène primitive, la rationalité n'étant pas encore complètement sortie de sa gangue mythologique. Ce caractère fondamentalement ambivalent contribue aussi sans doute à l'attrait particulier de ce récit.
Thalès, cela est rappelé, n’est pas Égyptien : c’est un « mathématicien et philosophe grec ». Le fait qu’il puisse appliquer son théorème en Égypte est aussi une manière d'en faire valoir la grande portée : les mathématiques sont grecques, mais elles s'appliquent aussi et sont efficaces jusqu'en Égypte. A cette portée géographique fait aussi écho une portée temporelle : c'est un théorème très ancien, antique, qui s'applique et s'enseigne toujours. Cette scène nous montre l’universalité des mathématiques en acte.
La rencontre de Thalès et du Pharaon est aussi la rencontre de l'élève avec Thalès, aussi bien le mathématicien que le théorème. Le récit peut lui donner l'impression que c'est Thalès lui-même qui lui enseigne son théorème. Il lui permet d'assister, comme dans un rêve, à son propre enseignement. C'est une rêverie qui lui est accordée en cours de mathématiques.
Cette page oppose un Thalès, mathématicien et philosophe grec, au Pharaon, Amasis (Ahmôsis), présenté comme incapable de mesurer la hauteur de la pyramide. Le savant grec va ainsi facilement résoudre un problème que ni le Pharaon, ni aucun autre Égyptien n'était en mesure de résoudre. L'histoire racontée valorise aussi l'élève : « Avec le théorème de ce chapitre, tu seras aussi fort que Thalès ». L'encart lui fait miroiter la possibilité qu'il devienne à son tour un Thalès grâce au théorème qui lui est enseigné. Il est incité à s'identifier à lui et à s'imaginer triompher des défis que les Pharaons pourraient lui lancer. Mais Thalès est, on l’a vu, présenté comme un mathématicien et philosophe grec. Une référence à la Grèce et à sa culture est introduite et en jeu (« mathématicien et philosophe »). Le pharaon représente quant à lui les Égyptiens ; le titre de « pharaon » leur est propre, comme les pyramides... Cette référence aux Égyptiens est confirmée et renforcée par l'indication que « personne ne pouvait mesurer la hauteur » ; comme il est entendu que Thalès va réussir, le lecteur doit donc comprendre que « personne » signifie « personne en Égypte » (plutôt que « personne au monde », par exemple). En devant compléter cette ellipse, il actualise la référence à l'Égypte ; l'opposition entre les deux civilisations est ainsi thématisée. Nous assistons donc à la confrontation de la connaissance du mathématicien-philosophe grec au pouvoir du monarque égyptien, de la culture grecque et de la culture égyptienne, la science étant associée à la Grèce et l'ignorance à l’Égypte : le Pharaon, pas plus qu'aucun autre Égyptien, n'est présenté comme « mathématicien et philosophe ». Qui aura d'ailleurs entendu parler d'un mathématicien et philosophe égyptien ?! L'élève est ainsi amené à s'identifier à celui qui connaît le théorème, c'est-à-dire au savant grec et à se sentir ainsi supérieur aux Égyptiens ignorants, de la base jusqu'au sommet de leur pyramide.
Ainsi Thalès est un savant grec et les Égyptiens sont ignorants. Soit... Mais Thalès n'est pas en Grèce, son pays, il est en l'occurrence en Égypte. Cela, on l'a vu, fait ressortir la grande portée de ce théorème. C'est un savant en terre étrangère, et plus précisément un savant dans un pays qui, pour les élèves, apparaîtra comme lointain et qui leur est présenté comme peuplé d'ignorants. On a là, il faut bien l'admettre, un faisceau de traits associés à la colonisation : l’Égypte après avoir été le théâtre de la compagne napoléonienne de 1798 a d’ailleurs bien été à la fin du 19e siècle une des plus importantes colonies britanniques rapidement disputée par l'Empire allemand.
La mesure de la hauteur de la pyramide par Thalès nous est présentée comme un fait historique. Un tel fait ne peut être connu que par des sources, c’est-à-dire des documents conservés (textes, peintures, etc.) qui nous ont été transmis d’une manière ou d’une autre et qui relatent cette mesure. Les encarts, s’ils ne sont pas purement imaginaires, en sont nécessairement directement ou indirectement inspirés. Il nous faut commencer par déterminer ces sources.
Une recherche sur internet ou/et dans une bibliothèque permet assez rapidement de repérer les sources des auteurs qui traitent de ces sujets. On peut d’ailleurs inversement écarter sans hésiter les livres ou les sites qui n’en indiquent aucune. Des encyclopédies comme Wikipedia, l’Encyclopaedia Universalis ou une recherche à partir d’un moteur de recherche peuvent être des points de départ utiles pour repérer ces sources. On trouve par exemple dans l’article « Thalès » de wikipedia, les deux références suivantes :
La recherche de « Thalès » dans l’Encyclopaedia Universalis nous renvoie à l’article « Antiquité – Naissance de la philosophie ». On retrouve dans la bibliographie de cet article la référence aux Présocratiques de Jean-Paul Dumont dans la Bibliothèque de la Pléiade. Reportons-nous donc à cette édition. Dans la note qui la présente, on peut lire qu’il s’agit en fait d’une traduction, on pouvait s’en douter…, des textes réunis par Hermann Diels dans les Fragmente der Vorsokratiker dont la première édition date de 1903. Cette référence aux Fragmente der Vorsokratiker de Diels figure d’ailleurs aussi dans l’article de l’Encyclopædia Universalis, On trouve en ligne de larges extraits de la deuxième édition, publiée en 1906. En voici la première page, justement consacrée à Thalès, qui réunit les fragments se rapportant à sa vie et son enseignement :

Même si on ne lit pas le grec, il est utile de consulter ces éditions ne serait-ce que pour voir en quoi elles consistent. Des rudiments dans cette langue permettent ensuite souvent de découvrir certains choix dans la traduction que nous lisons. On pourrait d’ailleurs s’interroger aussi sur les sources utilisées par Hermann Diels : Comment se présentent par exemple les fragments dont il dispose ? A-t-on conservé les manuscrits originaux ? Et sinon, de quand datent les copies conservées ? Dans quel état sont-ils et quelle part d’interprétation entre dans leur transcription ? Que les fragments soient donnés en grec ne suffit pas en effet à en garantir l’authenticité... Il suffit d’ailleurs de penser qu’il peut en exister plusieurs copies, susceptibles de présenter des différences (il ne s’agit pas de photocopies...), Diels devant alors faire des choix et composer un texte qui peut ne correspondre exactement à aucun des manuscrits conservés. Son édition serait bien en grec, mais elle présenterait finalement un texte dont il est pour une part l’auteur. Les mêmes questions se reposent pour leur traduction en français. Mais cela veut aussi dire inversement que lire le grec, même si cela est évidemment préférable, n’élimine pas les questions qui se posent avec la traduction : une édition en grec est à bien des égards elle-même déjà une traduction. Quoiqu’il en soit, connaître la réponse à ces questions peut être nécessaire si notre interprétation d’un fragment dépend du choix d’un mot précis, transcrit ou traduit. A défaut de les connaître, il est plus prudent de ne pas trop faire dépendre notre lecture de choix qui risquent d’être le fait de l’éditeur ou du traducteur.
Comme il s’agit à l’origine de manuscrits, la recherche des sources prend ici une forme particulière. Les questions posées changent avec le livre imprimé, c’est-à-dire à partir de 1450. Mais la nécessité d’identifier les sources disponibles et de les consulter demeure de toute façon.
Examinons à présent la traduction de Jean-Paul Dumont des fragments relatifs à la mesure de la pyramide dans l’édition de la Pléiade :

Le premier fragment est celui de Pline :

Cette source date du Ier siècle après J.-C. D’après les fragments cités, c’est la plus ancienne faisant référence à la mesure de la hauteur de la pyramide par Thalès. Les sources antérieures qui le citent ne font pas référence à cette mesure. Ni Hérodote (Ve siècle av. JC), ni Aristote (IIIe siècle av. JC), par exemple, n’en parlent. Il s’agit donc d’un témoignage tout de même postérieur de plus de sept siècles aux faits relatés... Il nous est rapporté par Pline (23 – 79 ap. J.-C), auteur romain, dans son Histoire naturelle (Livre XXXVI, 82), texte monumental comprenant trente sept Livres (un Livre correspond à un rouleau de papyrus). La seule indication est donc que Thalès a mesuré l’ « ombre à l’heure où elle est régulièrement égale à son objet». Reconnaissons que la traduction donnée, notamment l’ « ombre (…) égale à son objet », n’est pas très claire. C’est, quoi qu’il en soit, tout ce qui est précisé.
Il n’est pas difficile de trouver une autre traduction de ce passage, par exemple celle d’Emile Littré (1850) :

La traduction est assez différente de celle de Jean-Paul Dumont. Cette fois Thalès « mesura l’ombre à l’heure où elle est égale aux corps ». Il n’est plus question d’ « objets », mais de « corps ». Cela peut conduire à des interprétations différentes du procédé de mesure utilisé : on peut avec le terme « corps » introduire une référence au corps de Thalès, ce que ne permet guère celui d’ « objet ». On découvre aussi que le fragment traduit par Jean-Paul Dumont n’est en fait qu’une partie d’un texte bien plus vaste. On aurait pu penser qu’il s’agissait de toute la traduction du fragment conservé. La lecture du paragraphe complet l’inscrit dans une perspective qui n’était sans doute pas celle que l’on s’imaginait. Ce paragraphe figure en effet dans le Livre consacré au recensement des... monuments en pierre ! Son propos n'est pas vraiment mathématique. Et s'il y est question d'« un difficile problème », ce n'est pas celui de la mesure de la pyramide, mais celui de l’élévation des pierres pour sa construction. Pline semble accorder plus d’attention à la résolution de ce problème qu’à la mesure de la pyramide. La présentation sous forme de fragment, au côté d’autres fragments, à la fois décontextualise et re-contextualise le texte de Pline consacré à la construction de monuments en pierre. On peut et on doit à présent envisager qu’une dé/re-contextualisation semblable a pu être opérée pour les autres fragments.
Le deuxième fragment est celui de Plutarque (c.a. 46 – c.a. 125) :

La description de la mesure donnée par Plutarque est plus précise que celle de Pline. Il est cette fois fait référence à un bâton, au lieu d’un « objet » ou d’un « corps », dont il est précisé qu’il doit être placé à la fois « à plomb » et à l’extrémité de l’ombre de la pyramide. Il est aussi indiqué que l’on obtient ainsi deux triangles et que la hauteur de la pyramide, la hauteur du bâton, et leurs ombres respectives sont proportionnelles. On n’y trouve en revanche aucune référence à un quelconque Pharaon.
On peut se reporter à l’édition de Diels dont l’édition de la Pléiade est la traduction. Les fragments de Pline et de Plutarque se présentent comme suit :

Les deux extraits de Pline et de Plutarque sont donnés comme un seul fragment, présentés sous le même numéro 21, repris dans l’édition de Dumont, mais dans deux paragraphes successifs distincts. Sans être un latiniste, on peut tout de même remarquer que le fragment en latin comprend le terme « corpori ». Sa traduction par « corps », adoptée par Littré, apparaît plus littérale que celle par « objets », adoptée par Dumont.
On trouve un récit similaire dans un fragment de Diogène Laërce, soit au début IIIe siècle ap. J.C., c’est-à-dire deux siècles après Pline et Plutarque :

La source de Diogène est Hiéronyme, auteur cité notamment par Cicéron. Ce fragment est extrait de la partie des Vies et doctrines des philosophes illustres consacrée à Thalès. Cette fois l’extrait donné par Diels et traduit par Jean-Paul Dumont est bien plus long que celui que nous citons.
Voilà, l’ensemble des fragments traduits par Jean-Paul Dumont relatifs à la mesure de la pyramide par Thalès ont été recensés et cités. On peut à présent les lire d’un peu plus près.
Revenons au fragment de Plutarque. Il est lui aussi extrait d’un texte plus étendu intitulé Le Banquet des Sept Sages. On peut en citer un plus large extrait. Il nous faut pour cela en considérer une autre traduction. Un des personnages du Banquet s’adresse à Thalès en ces termes :

Cette citation plus longue que le fragment traduit dans la Pléiade fait bien à présent apparaître le nom du Pharaon Amasis. C’est de fait la seule source qui mentionne ce Pharaon avec la mesure de la pyramide par Thalès. Mais voyons plus précisément ce qu’il en est.
Le Banquet des Sept Sages, dont cette citation est extraite, est un dialogue imaginaire qui se tient à l’occasion d’un banquet qui réunit les sept sages, dont Thalès (leur liste varie : Solon, Bias, Thalès, Anarcharsis, Cléobule, Pittacos, Chilon, Périandre). Le passage relatant la mesure de la pyramide se trouve au début. Il vaut la peine de lire l’intégralité du texte qui précède ce passage :

Voir aussi l'édition bilingue, grec-français sur le site renacle.org
Il apparaît que Dioclès rapporte à Nicarque les propos échangés lors d’un banquet qui a réuni les sept sages auquel il a lui-même participé. Ce banquet est organisé par Périandre, tyran de Corinthe, dans le port où se trouve le temple de Vénus à l’occasion du sacrifice qu’il va y faire à la mémoire de sa mère « victime d’un malheureux amour ». Plusieurs allusions indiquent que Dioclès est devin de profession. Une note en bas de page précise l’amour qui poussa la mère de Périandre à se suicider :

Diogène Laërce en fait le récit suivant dans la partie des Vies et doctrines des philosophes illustres consacrée à Périandre :

Le banquet serait donc organisé à l’occasion d’un sacrifice que le tyran de Corinthe va faire suite au suicide de sa mère avec laquelle il a entretenu une relation amoureuse. Dioclès qui, à la demande de Périandre, avait hébergé Thalès pour l’occasion se rend au banquet avec lui. Bien que des chars aient été mis à leur disposition par Périandre pour les conduire au port, Thalès préféra, malgré la grande chaleur, se rendre au banquet à pieds avec son hôte. Ils sont rejoints en chemin par Niloxène, que Thalès a bien connu en Égypte, et qui est porteur d’une lettre du Pharaon Amasis. Cette lettre n’est pas adressée à Thalès, mais à Bias, un autre des sept sages qui assistera aussi au banquet. Niloxène n’en connaît pas encore le contenu, mais il se doute qu’il s’agit d’une nouvelle énigme, comme la suite le confirmera. Le Pharaon et le roi d’Éthiopie s’envoient en effet régulièrement des énigmes pour s'éprouver mutuellement. Le Pharaon a « toujours vaincu jusqu'à présent » le roi d’Éthiopie (p. 337), mais l’énigme cette fois néanmoins lui résiste ; il n’est pas certain de sa réponse et c’est sans doute à nouveau pour solliciter son aide qu’il écrit à Bias. Il l’avait en effet déjà sollicité pour une précédente énigme : il lui avait alors envoyé une victime en lui demandant de couper ce qu’il y avait chez elle de meilleur et de plus mauvais, puis de lui renvoyer ces deux parties. La réponse de Bias consista à ne renvoyer que la langue au Pharaon, signifiant ainsi qu’elle était à la fois ce que l’homme avait de meilleur et de plus mauvais. Telle était l’énigme et telle avait été la réponse donnée par Bias qui lui fit obtenir « l’estime et l’admiration » du Pharaon. Peut-être la sagesse de Bias a-t-elle consisté en l’occurrence à trouver une réponse qui lui a permis de préserver la vie de la victime, ce qui n’aurait pas été le cas s’il avait considéré que le cœur ou la tête en était la meilleure partie. Quoiqu’il en soit, c’est bien de « l’estime et de l’admiration » dont il s’agit, et plus précisément de « l’estime et de l’admiration » dont un sage peut être l’objet de la part d’un tyran. L’opposition est bien aussi entre un sage et un tyran, et non un savant et un Pharaon ignorant. Thalès est la figure du sage, le plus ancien d’entre-eux, et participe à ce banquet à ce titre. C’est aussi à ce titre, en tant qu’un des sept sages, que Diogène Laërce lui consacre le plus long témoignage qui nous soit parvenu. Et son texte commence par indiquer d'autres auteurs qui en ont traité au même titre. Quoiqu’il en soit, on voit quelle a été l’énigme et la réponse qui ont valu à Bias ces honneurs de la part du Pharaon. Niloxène fait alors valoir que Bias, contrairement à Thalès, auquel il s’adresse en présence de Dioclès qui rapporte la scène, ne dédaigne pas l’amitié des rois. C’est bien d’ailleurs à Bias que le Pharaon écrit, le qualifiant de « le plus sage des Grecs » (p. 337), et non à Thalès. C’est là d’ailleurs, lui dit Niloxène, la deuxième raison qui vaut à Bias « l’estime et l’admiration » du Pharaon, rappelant à Thalès qu’il est lui au contraire connu pour ses propos injurieux à l’encontre des tyrans dont il nous donne quelques échantillons. Mais Niloxène fait néanmoins valoir qu’il a pourtant lui aussi « l’estime et l’admiration » de celui-ci et cela justement pour avoir mesuré la hauteur de la pyramide. C’est donc dans ce contexte et à ce titre que le récit de cette mesure est rapporté. Comme Niloxène s’adresse à Thalès, son propos n’est pas de lui en faire connaître la possibilité, ni non plus de lui en exposer les modalités, mais de lui signifier, et cela plutôt pour l’embarrasser, qu’il a de ce fait, lui aussi, et malgré lui, « l’estime et l’admiration » de ce Pharaon-tyran qui échange des énigmes avec le roi d'Éthiopie.
Nulle part il n’est dit ou seulement suggéré que les Égyptiens ne savaient pas effectuer cette mesure. C’est la simplicité du procédé, et plus précisément le fait que la mesure ait pu être réalisée « sans aucun instrument mathématique » qui, dans ce récit de Plutarque, a suscité l’admiration du Pharaon. Il n’est non plus nulle part question d’un défi lancé par le Pharaon à Thalès. Le Pharaon échange bien des énigmes mais c’est avec le roi d’Ethiopie. Il ne fait que consulter Bias, et non Thalès, à leur propos. En outre, une énigme est délibérément formulée de termes sibyllins et la résoudre consiste en premier lieu à en trouver le sens ; la mesure de la pyramide n’est pas de la nature d’une réponse à une énigme. Dans la seconde énigme, révélée plus loin au cours du banquet (p. 337), le roi d’Éthiopie demande au Pharaon de boire toute la mer ; s’il satisfait cette demande il lui cédera plusieurs villes de son royaume, sinon le Pharaon devra lui céder une partie du sien. La solution en sera discutée au cours du banquet. Si l’aide du sage peut être sollicitée, la nature des énigmes et leurs enjeux (la mort d’un homme ou la cession de parties d’un royaume), suppose de disposer à sa guise de la vie d’un homme et des terres d’un royaume qui sont des prérogatives de tyrans et non de sages. Il est d’ailleurs rappelé (p. 343) que les énigmes ont à l’origine été une tradition grecque qui avait servi à départager Homère et Hésiode lors d’un concours de poésie au terme duquel les juges n’avaient pas trouvé d’autre moyen pour les départager. Il s’agissait à nouveau de départager deux personnes de même qualité, ce qui n’est pas le cas de Thalès et du Pharaon.
Les dialogues sont en l’occurrence des propos rapportés par Dioclès, adressés à Nicarque. Il a fallu pour le savoir lire le texte depuis le début. Le récit de la mesure de la pyramide est ainsi un propos de Niloxène, rapporté par un devin de profession dans une œuvre de fiction de Plutarque. Les indications sur la mesure sont attribuées à Niloxène, qui s’adresse directement à Thalès, qui est celui qui a le moins besoin qu’on lui en rappelle les détails… Ces indications peuvent être le fait de Dioclès à l’intention de Nicarque auquel il s’adresse. Elles peuvent enfin être le fait de Plutarque à l’intention de son lecteur. Dans tous les cas Plutarque en est certes in fine l’auteur, mais le statut et l’analyse que l’on peut en faire changent selon que l’on prend en compte ou non la part possible des différents énonciateurs dans l’énoncé qui en est donné. Selon la longueur de l’extrait que l’on retient, le récit de la mesure de la pyramide pourra aussi apparaître comme un témoignage de Plutarque, un propos de Niloxène rapporté par Plutarque, ou enfin, pour ce qu’il est, c’est-à-dire un propos de Niloxène, qui s’adresse à Thalès, rapporté par Dioclès dans un dialogue fictif de Plutarque traduit en français par Jean-Paul Dumont à partir d’une édition grecque de Hermann Diels du début du 20e siècle. Cela n’exclut pas que la description puisse être dans une certaine mesure authentique. Il est néanmoins impossible de le déterminer à partir de ce seul texte, comme il est impossible de savoir uniquement à partir de celui-ci si les personnes citées désignent des personnes réelles ou fictives. Il faudrait au minimum étudier d’autres récits du même genre pour pouvoir espérer apprécier le statut attendu des faits et des personnes cités. Le risque serait de prendre des faits relatés par Dark Vador dans un épisode de Star Wars pour des faits historiques (ce qu’ils pourraient bien être parfois!) ou inversement de considérer des documents d’archives pour des œuvres de fiction. Toutes les combinaisons étant en outre possibles. Il est de toute façon difficile de déterminer le genre d’un texte hors de son contexte. Ainsi, peu avant le banquet, Périandre fait appeler Dioclès et Thalès pour leur montrer ce qu’un jeune homme lui a apporté. Il s’agit en l’occurrence d’un enfant centaure : « il disait être né d’une cavale, qui avait la tête, le cou et les mains d’un homme, et dans tout le reste, était fait comme un cheval ». Tous les faits rapportés, même ceux dont Dioclès est directement témoin, ne semblent donc pas devoir être tenus pour authentiques… Il serait à nouveau assez difficile de déterminer si le lecteur est censé croire ou non en l’existence de centaures. Cela change pourtant l’interprétation de ce passage, voire de l’ensemble du texte. Niloxène est effrayé à la vue de ce centaure, Thalès s’en amuse, mais la possibilité de son existence n’est pas remise en cause ni par l’un ni par l’autre. Au contraire, elle permet de prêter un nouveau trait d’esprit à Thalès qui suggère à Périandre de ne plus faire garder ses juments par de trop jeunes bergers ou de les marier : « je pense que vous ne devez pas avoir, pour garder vos juments, des bergers aussi jeunes, ou que vous devez les marier. » (p. 333-334).
L’encart du Nouveau Prisme, comme la plupart des encarts rapportant la mesure de la pyramide par Thalès, sont des variations sur le thème de la rencontre d’un savant grec et d’un Pharaon égyptien ignorant. Cette présentation est remarquable parce que toutes les sources disent exactement l'inverse ! Il suffit pour le découvrir de poursuivre un peu notre lecture de l’édition française des fragments présocratiques.
Ainsi, Flavius Josèphe (Ier s. ap. J.-C) écrit dans Contre Apion, I, 2 (Dumont, p. 14) :
Tout le monde s'accorde à reconnaître que les premiers chez les Grecs à avoir étudié les choses célestes et divines, comme Phérécyde de Syros, Pythagore et Thalès, furent les élèves des Égyptiens et des Chaldéens
Diogène Laërce, citant Pamphile, présente aussi Thalès comme « ayant étudié la géométrie auprès des Égyptiens » (Diogène Laërce, p. 82 ; Dumont, p. 14).
De même, Jamblique (IIIe-IVe s. ap. J.-C), dans la Vie pythagorique, 12 (p. 15) :
Thalès conseilla à Pythagore de se rendre en Égypte et de s'entretenir le plus souvent possible avec les prêtres de Memphis et de Disopolis : c'est d'eux qu'il avait tiré toutes ses connaissances qui le font passer pour sage et savant aux yeux de la foule.
Aétius (Ve s. ap. J.-C) ne dit pas autre chose dans ses Opinions, I, III,1 (Dumont, p. 15) :
Il étudia la philosophie en Égypte et revint à Milet déjà fort âgé
Suivant toutes ces sources, Thalès est donc allé en Égypte plutôt en élève qu'en maître : il est allé en Égypte pour y chercher le savoir plutôt que pour le diffuser. Thalès n'y apparaît pas comme un missionnaire allant en Égypte chargé d'y transmettre ses connaissances, mais comme un homme revenant d’Égypte fort des connaissances qu’il y a acquises.
Suivant de nombreuses sources grecques antiques, la géométrie a elle-même son origine en Égypte. Ainsi, Hérodote (Ve s. av. J.-C) écrit-il (Enquête, II, 109, Dumont, p. 15) :
C’est [en Égypte], à mon avis, que la géométrie fut inventée, et c’est de là qu’elle vint en Grèce.
On peut d’ailleurs citer le paragraphe complet, cette fois dans la traduction de Larcher, publiée en 1850, et disponible en ligne :

Proclus écrit (Ve, Les commentaires sur le premier livre des Éléments d'Euclide, 65, 3, trad. Paul ver Eecke, 1948, p. 55-56):
or, comme nous devons considérer les débuts des sciences et des arts dans la période actuelle, nous dirons que beaucoup d'auteurs rapportent que la géométrie, née de la mesure des terrains, a été inventée par les Égyptiens, et que cette mesure leur était nécessaire à cause de la crue du Nil qui faisait disparaître les bornes appartenant à chacun. Il n'est d'ailleurs pas étonnant que l'invention de cette science et des autres ait été commandée par l'intérêt ; car tout ce qui est obtenu dans la génération procède de l'imparfait au parfait. Il est donc naturel qu'une transition se produise de la sensation au raisonnement et de celui-ci à l'intelligence. Dès lors, de même que la connaissance exacte des nombres a pris sa source chez les Phéniciens à cause du commerce et des transactions, la géométrie a de même été trouvée par les Égyptiens pour la raison que nous venons de dire. Thalès fut le premier Grec qui, ayant été en Égypte, en rapporta la théorie dans l'Hellade ; il trouva beaucoup de choses lui-même et fit connaître les principes de nombre d'entre elles à ses successeurs en s'appliquant aux unes de manière plus générale et aux autres d'une manière plus sensible.
Platon aussi bien qu'Aristote, devenus depuis parmi les plus éminents représentants du savoir grec, nous font eux aussi le récit plus général d'une science ayant son origine en Égypte ! Leurs récits respectifs diffèrent l’un de l’autre à tous égards à l'exception d'un seul point : la science aurait été transmise aux Grecs par les Égyptiens. Ainsi, dans le Phèdre de Platon (274c-275b, traduction Léon Robin, Bibliothèque de la pléiade) :
Socrate : Ce qu'on m'a donc conté, c'est que, dans la région de Naucratis en Égypte, a vécu un des antiques Dieux de ce pays-là, celui dont l'emblème consacré est cet oiseau qu'ils nomment l'ibis, et que Theuth est le nom de ce Dieu; c'est lui, me disait-on, qui le premier inventa le nombre et le calcul, la géométrie et l'astronomie, sans parler du trictrac et des dès, enfin précisément les lettres de l'écriture. Or, d'autre part, l'Égypte entière avait pour roi en ce même temps Thamous, qui résidait dans la région de cette grande ville du haut pays que les Grecs appellent Thèbes d'Égypte, comme Thamous est pour eux le Dieu Ammon. Theuth, s'étant rendu prés du roi, lui présenta ses inventions, en lui disant que le reste des Égyptiens devrait en bénéficier. Quant au roi, il l'interrogea sur l'utilité que chacune d'elles pouvait bien avoir, et, selon que les explications de l'autre lui paraissaient satisfaisantes ou non, il blâmait ceci ou louait cela. Nombreuses furent assurément, à ce qu'on rapporte, les observations que fit Thamous à Theuth, dans l'un et l'autre sens, au sujet de chaque art, et dont une relation détaillée serait bien longue. Mais, quand on en fut aux lettres de l'écriture :
"Voilà, dit Theuth, la connaissance, ô Roi, qui procurera aux Égyptiens plus de science et plus de souvenirs ; car le défaut de mémoire et le manque de science ont trouvé leur remède!" A quoi le roi répondit: "Ô Theuth, découvreur d'arts sans rival, autre est celui qui est capable de mettre au jour les procédés d'un art, autre est celui qui l'est, d'apprécier quel en est le lot de dommage ou d'utilité pour les hommes appelés à s'en servir! Et voilà maintenant que toi, en ta qualité de père des lettres de l'écriture, tu te plais à doter ton enfant d'un pouvoir contraire de celui qu'il possède. Car cette invention, en dispensant les hommes d'exercer leur mémoire, produira l'oubli dans l'âme de ceux qui en auront acquis la connaissance; en tant que, confiants dans l'écriture, ils chercheront au-dehors, grâce à des caractères étrangers, non point au-dedans et grâce à eux-mêmes, le moyen de se ressouvenir; en conséquence, ce n'est pas pour la mémoire, c'est plutôt pour la procédure du ressouvenir que tu as trouvé un remède. Quant à la science, c'en est l'illusion, non la réalité, que tu procures à tes élèves: lorsqu'en effet, avec toi, ils auront réussi, sans enseignement, à se pourvoir d'une information abondante, ils se croiront compétents en une quantité de choses, alors qu'ils sont, dans la plupart, incompétents; insupportables en outre dans leur commerce, parce que, au lieu d'être savants, c'est savants d'illusion qu'ils seront devenus!"
Aristote (384-322), dans sa Métaphysique, 981 b 13-24, trad. J. Tricot, Vrin, 2000, p. 5, écrit :
C'est donc à bon droit que celui qui, le premier, inventa un art quelconque, dégagé des sensations communes, excita l'admiration des hommes ; ce ne fut pas seulement à raison de l'utilité de ses découvertes, mais pour sa sagesse et pour sa supériorité sur les autres. Puis les arts se multiplièrent, ayant pour objet, les uns, les nécessités, les autres, l'agrément ; toujours les inventeurs de ces derniers furent considérés comme plus sages que ceux des autres, parce que leurs sciences n'étaient pas dirigées vers l'utile. - Aussi tous les différents arts étaient déjà constitués, quand on découvrit enfin ces sciences qui ne s'appliquent ni aux plaisirs, ni aux nécessités, et elles prirent naissance dans les pays où régnait le loisir. C'est ainsi que l'Égypte fut le berceau des Mathématiques, car on y laissait de grands loisirs à la caste sacerdotale.
Nous avons lu tous les fragments anciens relatifs à la mesure de la pyramide par Thalès édités par Diels et traduits par Jean-Paul Dumont. Aucun d’eux n'indique précisément le théorème utilisé par Thalès. Dans le plus ancien, Pline ne mentionne pas de proportion. Il indique en revanche que la mesure a été faite quand la hauteur du bâton était égale à son ombre. Or, cette condition dispense de recourir à la notion de proportion associée au « théorème de Thalès ». Plutarque utilise lui une proportion (« vous démontrâtes qu'il y avait la même proportion »), plutôt qu'une simple égalité ; les conditions pour réaliser la mesure sont corrélativement plus simples. Il est aussi le seul à faire mention du Pharaon. Dans le récit de Diogène Laërce, une personne tient lieu de bâton et participe à ce titre au dispositif de mesure. Des ouvrages cités, l'Histoire naturelle de Pline est le seul ayant un caractère un peu technique. Le banquet des sept sages de Plutarque est quant à lui le récit fictif d'un banquet réunissant les sept sages grecs. La citation de Diogène Laërce est extraite du premier Livre des Vies et doctrines des philosophes illustres consacré à une présentation de chacun de ces sept sages. Thalès en tant que plus ancien est traité en premier. Aucun de ces ouvrages ne donne et n'a vocation à donner une description effective de la mesure de la hauteur de la pyramide.
Considérons à présent les références à Thalès dans les traités mathématiques. Aucun d’eux, bien sûr, ne mentionne la mesure de la pyramide. Les Commentaires philosophiques et mathématiques sur le livre premier des Éléments d'Euclide de Proclus (Ve siècle ap. JC) sont ici notre principale source. On peut à nouveau recenser tous les passages dans lesquels Proclus attribue un théorème à Thalès :
« On rapporte que Thalès a été le premier à démontrer que le cercle est coupé en deux parties égales par le diamètre » Proclus, p. 139
« Grâces soient donc rendues à Thalès, tant pour son invention de beaucoup d'autres théorèmes que celui-ci [égalité des angles à la base des triangles isocèles] ; car on dit qu'il fut le premier à penser et à affirmer que les angles situés à la base de tout triangle isocèle sont égaux, et à exprimer d'une manière plus surannée que les angles égaux sont semblables. » Proclus, p. 216-217
« Ce théorème, que Thalès a trouvé d'abord et que l'Auteur des Éléments a jugé digne d'une démonstration scientifique, montre que si deux lignes droites se coupent mutuellement, les angles placés au sommet sont égaux. » Proclus, p. 255
Et enfin :
« Eudème, dans ses Histoires géométriques, attribue le présent théorème à Thalès [égalité des triangles : deux angles et un côté égaux] ; car, déclare-t-il, il est nécessaire de faire usage de ce théorème pour reconnaître la distance des bateaux en mer de la manière qui a été montrée par Thalès. » Proclus, p. 300
Proclus lui attribue directement les trois théorèmes suivants :
Diogène Laërce, quant à lui, lui attribue l'inscription d'un triangle rectangle dans un cercle :
« il fut le premier à avoir circonscrit un triangle rectangle dans un cercle », Diogène Laërce, p. 82 Diogène Laërce, p. 82
On obtient la même liste des théorèmes qui lui sont attribués dans la notice consacrée à Thalès dans l’Encyclopædia Universalis (avec l’indication de la source en plus…), dans laquelle ne figure pas non plus le « théorème de Thalès »
Le « théorème de Thalès » ne fait donc pas partie de ceux que Proclus attribue à Thalès. Il ne semble pas non plus qu’Eudème le lui attribue dans ses Histoires géométriques que cite Proclus. Les théorèmes qui lui sont attribués ne traitent donc que d'égalité de figures ou d'angles ; la notion de proportion n'intervient dans aucun d'eux. Mais il faut nuancer cette observation en la recontextualisant elle aussi en tenant compte des sources : les commentaires de Proclus portent en effet sur le premier Livre des Éléments d'Euclide. Or, si l’on s’y reporte, on peut constater qu’il est lui-même exclusivement consacré à l'égalité des figures ! La notion de proportion n’est introduite qu’au Livre V des Eléments et l’énoncé correspondant à notre « théorème de Thalès » s’y trouve bien, mais seulement dans le Livre VI. Il se peut donc tout à fait que Proclus ne le cite pas simplement parce qu’il n’est pas dans le Livre I dont il s’occupe. Le recensement des théorèmes attribués à Thalès effectué à partir du commentaire de Proclus doit donc aussi tenir compte de son propos limité au seul Livre I des Eléments. On risque autrement d’attribuer aux mathématiques de Thalès une restriction qui viendrait en fait du propos de cette source. Il est en l’occurrence nécessaire pour cela de se reporter aux Eléments d’Euclide, pourtant bien postérieurs à Thalès ! Une liste de théorèmes, comme celle donnée dans l’article de l’Encyclopædia Universalis, est donc difficilement utilisable sans l’indication des sources qui ont servi à l’établir. Mais cela ne suffit pas : il faut encore citer ces sources et non seulement en donner la référence. Mais l’exemple de Proclus, comme déjà celui de Plutarque, montre que cela ne suffit pas non plus : il faut encore connaître le propos de l’auteur cité pour apprécier la valeur des citations données et l’usage qu’il est possible d’en faire...
Quoiqu’il en soit, seul Plutarque mentionne une proportion et peut s'affranchir de la condition d'égalité entre le bâton et son ombre pour mesurer la hauteur de la pyramide. Cette condition d'égalité, mentionnée à la fois par Pline et Diogène Laërce, est inversement inutile si le « théorème de Thalès » est appliqué : au moment où l'ombre du bâton est égale au bâton, l'ombre de la pyramide est aussi égale à la hauteur de la pyramide. Pour obtenir cette hauteur, il n’y a plus qu'à mesurer l'ombre projetée au sol (la partie inaccessible de cette mesure s'obtenant à partir de la longueur de la base de la pyramide). Le « théorème de Thalès » n’intervient pas dans ce raisonnement. Il suffit de savoir qu'un triangle rectangle dont les deux angles non droits sont égaux est isocèle. C'est là un théorème exactement du même genre que ceux attribués à Thalès. Le « théorème de Thalès » n'est donc pas nécessaire pour mesurer la hauteur de la pyramide suivant les indications données par Pline et Diogène Laërce ; son usage rendrait superflue l’égalité du bâton et de son ombre, la seule indication précise qu’ils donnent!
La dernière citation de Proclus se réfère à l'Histoire de la géométrie, ouvrage aujourd'hui perdu d'Eudème, élève d'Aristote. Il ne s’agit plus cette fois de la mesure de la hauteur de la pyramide, mais de celle de la distance au rivage d'un bateau, aussi souvent donnée dans les manuels comme exemple d’application du « théorème de Thalès ». Eudème n'a visiblement lui-même pas plus d'indications que nous sur le théorème utilisé et doit donc lui-même spéculer sur la manière dont Thalès a pu procéder. Cependant, il n'en déduit pas qu’il aurait utilisé le « théorème de Thalès », mais un théorème bien plus élémentaire, en l'occurrence un des cas d'égalité des triangles. Et en effet, comme pour la hauteur de la pyramide, la distance d'un navire au rivage peut être obtenue au moyen de triangles isocèles (Voir par exemple : https://www.lozedion.com/wp-content/uploads/2013/09/Thal%C3%A8s03.pdf). Le « théorème de Thalès » n'est pas nécessaire à ces mesures. Une fois remis en cause ce préjugé, à l’œuvre dans la plupart des encarts inspirés de ces récits, il n’est pas difficile d’en proposer des solutions alternatives.
La lecture des sources à laquelle nous venons de nous livrer ne procède pas d’une forme de culte de l’origine ou de l’authentique. Les conditions de transmission et d’édition des extraits cités de Pline, de Plutarque ou de Diogène Laërce obligent à renoncer à toute idée d’originalité et d’authenticité. Mieux on les connaît, plus les idées d’originalité et d’authenticité se dissolvent. Même la langue dans laquelle nous les lisons, fût-elle le grec ou le latin, ne peut prétendre être leur langue d’origine ; les langues ont aussi une histoire. On a pu voir l’intérêt de lire un plus large extrait, voire l’intégralité, du Banquet des sept sages de Plutarque pour éviter un usage incorrect de la citation qui en est extraite. Mais il est aussi apparu que cela ne suffisait pas. Cela ne permet pas, par exemple, de déterminer si celui qui rapporte ces propos est un personnage fictif ou non. Or, il s’agit en l’occurrence de propos de Niloxène rapportés par Dioclès dans une œuvre de Plutarque : la lecture intégrale du texte, même en grec, ne permettra jamais de trancher cette question dont dépend pourtant la valeur du fragment cité. De la même manière, il importe de rapporter la liste des théorèmes attribués à Thalès aux sources à partir desquelles elle a été établie. Mais à nouveau, s’il est nécessaire de préciser ces références, cela ne suffit pas. Il ne suffit pas en effet d’indiquer que Proclus attribue tel théorème à Thalès dans ses Commentaires philosophiques et mathématiques sur le livre premier des Eléments d'Euclide ; la liste obtenue dépend en l’occurrence aussi du propos de Proclus dans cet ouvrage, et en particulier au fait de se limiter au premier Livre des Eléments. Pour savoir ce que cela implique, il faut au moins aussi lire Euclide : on ne connaît pas sinon ce que cela implique. Et sans doute ne suffit-il pas de ne lire que le Livre I pour identifier ce qui le distingue des suivants. Si, par exemple, Proclus ne lui attribue aucun théorème sur les proportions, c’est peut-être simplement parce qu’ils ne sont pas exposés au Livre I. Le risque est sinon très réel de considérer que la nature des théorèmes que Proclus attribue à Thalès reflète exclusivement le niveau des mathématiques de Thalès quand elle reflète en fait aussi la nature des mathématiques du Livre I des Eléments d’Euclide.
Il ne saurait donc s’agir de chercher dans les sources la vérité, le fin mot de l’histoire. Si leur lecture a bien néanmoins à voir avec la vérité, c’est en un autre sens : elles nous font connaître la vérité de ce qui nous est dit, au sens où elles nous font connaître la valeur des encarts que nous lisons. Et elles sont pour cela nécessaires. C’est uniquement en les lisant que nous pouvons connaître la valeur du récit rapporté de la mesure de la pyramide et découvrir, par exemple, que l’une des principales sources est extraite d’une œuvre de fiction qui implique trois niveaux d’énonciation (Niloxène, Dioclès, Plutarque) dans laquelle les personnages rencontrent un centaure sans qu’aucun n’en remette en cause la possibilité. C’est aussi en lisant ces sources que nous avons pu remettre en cause l’évidence de la nécessité d’utiliser le « théorème de Thalès » pour la mesure de la pyramide qui est supposée dans la plupart des encarts et dans la lecture que nous en faisons volontiers. Se reporter aux sources nous a surtout permis de découvrir que de nombreux aspects du récit présenté dans l’encart ne se retrouvaient pas dans ces sources. Et à nouveau, la question n’est pas la fidélité aux sources, mais ce que ces différences nous font découvrir sur l’histoire qui nous est présentée dans les encarts actuels. Et cela, il aurait été impossible de découvrir autrement. Nous avons ainsi pu découvrir que la qualité de sage à laquelle est rapportée Thalès avait disparu au profit de celle de savant ; celle de tyran est aussi remplacée par celle d’ignorant. Les énigmes échangées entre les deux tyrans, le Pharaon et le roi d’Ethiopie, laissent place à un défi qui aurait été adressé par le Pharaon à Thalès. Le voyage entrepris par Thalès en Égypte pour s’y former est remplacé par l’expression d’un rapport de domination inverse, teinté de colonialisme, dans lequel un savant occidental montre sa science au monarque oriental ignorant. C’est en définitive l’ensemble du récit qui a été décontextualisé et re-contextualisé. Il n’était pas difficile de se douter que ce témoignage était pour le moins douteux, voire faux. Certains encarts le suggèrent. Mais ce qui est plus significatif, c’est la nature de la falsification opérée. Or, seule la lecture de ces sources permet d’identifier ce qui a été retranché et ajouté. Ce sont ces changements que les sources nous permettent de découvrir. Ces changements ont d’ailleurs sans doute été considérés comme anodins par ceux qui les ont opérés. Probablement n’ont-ils pas eu conscience de les faire trouvant sans importance ce qu’ils retranchaient et considérant que ce qu’ils ajoutaient y étaient au fond déjà ; ils n’ont fait que le faire ressortir un peu mieux, que grossir le trait... Ces récits ainsi modifiés conviennent aussi d’autant mieux à leurs lecteurs et sont de ce fait d’autant plus facilement repris et diffusés. Le fait que Thalès triomphe d’un défi lancé par le Pharaon grâce au « théorème de Thalès » joue bien un rôle essentiel dans l’intérêt que les élèves et nous-mêmes y trouvons. Cela correspond mieux au contexte scolaire et favorise tout un jeu d’identifications de la part aussi bien des élèves que de l’enseignant qui en fait son attrait et son efficacité. Mais comme ces modifications ont précisément été introduites pour rendre le récit plus satisfaisant, plus conforme à nos attentes et à nos préjugés, elles passent aussi de ce fait d’autant plus inaperçues qu’ils sont plus largement et profondément partagés. Si nous sommes enclins à considérer que la culture occidentale est supérieure à la culture orientale, le récit nous conviendra parfaitement et même nous confortera dans notre idée. Non seulement il ne nous heurtera pas, mais il nous satisfera et même, en l’occurrence, nous flattera, car c’est sans doute que nous nous identifions à cette culture. On peut ainsi constater que la plupart des auteurs de manuels semblent adhérer à ce point de vue et ce faisant participent à sa diffusion auprès des élèves : voilà bien, en revanche, un fait historique ! Si nous pensons que le « théorème de Thalès » est nécessaire pour mesure la hauteur de la pyramide, le récit nous conviendra aussi parfaitement. On peut inversement pour une raison ou une autre être d’emblée gêné par certains aspects du récit. Une familiarité antérieure avec d’autres cultures pourra par exemple nous faire réagir à la vision colonialiste à l’œuvre dans ce récit. Sans doute suffit-il par exemple d’être Égyptien pour réagir à cet aspect. Un certain rapport critique aux mathématiques peut aussi conduire à chercher des solutions alternatives à celle présentée comme étant la seule. Réunir ces deux compétences, si l’on n’est pas Égyptien..., s’avère sans doute déjà assez exceptionnel. La lecture des sources permet en l’occurrence à chacun de découvrir tout cela. Le retour aux sources ne procède donc nullement de la croyance que la vérité s’y trouverait, mais il est un puissant moyen pour découvrir certains des préjugés à l’œuvre dans notre représentation du savoir véhiculés par ces encarts et nos enseignements.
Si l’on ne sait pas quel théorème Thalès a utilisé, c’est en partie parce que ce n’était pas l’usage de faire référence aux théorèmes en leur attribuant des noms, propres ou non, comme nous le faisons. Si Pline, Plutarque et Diogène Laërce avaient écrit plus tard, ils auraient sans doute nommé le théorème utilisé. Ils ne l’auraient peut-être pas nommé le « théorème de Thalès », mais il lui aurait donné un nom. Il y avait bien un énoncé correspondant au théorème de Pythagore, mais pas de « théorème de Pythagore ». Il y a bien dans les Eléments d’Euclide un énoncé correspondant au théorème de Thalès, mais pas de « théorème de Thalès ». Ce n’est pas seulement que les dénominations « théorème de Thalès », « Théorème de Pythagore », « postulat d’Euclide », « algorithme d’Euclide », « axiome d’Archimède », etc. n’étaient pas introduites, c’est que l’usage de dénommer les théorèmes n’existait pas.
L'usage par Thalès du « théorème de Thalès » pour mesurer la hauteur de la pyramide ou la distance d'un navire au rivage une fois remis en cause, l'attribution de ce théorème à Thalès apparaît sans guère de fondement. Cela conduit à se poser la question de l'introduction de cette appellation particulière. D'après l'enquête réalisée par Henry Plane (1995, p. 79), la première occurrence de cette attribution se trouve dans la réédition de 1883 du Traité de géométrie élémentaire d'Eugène Rouché et Charles de Comberousse :
Le fait que ce nom ait ainsi été introduit en France vers la fin du 19ème siècle soulève naturellement la question des raisons de cette introduction, en France et à ce moment. Henry Plane avance pour y répondre l'hypothèse que ce serait un effet de l'injonction faite au début de la Troisième République aux candidats de l'agrégation de mathématiques d'avoir des connaissances en histoire de leur discipline :
Cette origine de l'usage de l'appellation « théorème de Thalès » est aussi donnée par le site de l'Irem de l'Université de Poitiers :

On y retrouve aussi, sans référence mais entre guillemets, l'explication selon laquelle cette attribution viendrait de « l'incitation faite aux agrégatifs à la fin du XIXe siècle d'attribuer aux résultats des noms de mathématiciens pour qu'ils s'intéressent à l'histoire des mathématiques » :

La date et l'origine de l'appellation « théorème de Thalès », avec la même explication, sont aussi reprises dans l'article de Wikipedia sur le « théorème Thalès » (qui renvoie au site de l'Irem de Poitiers) :

L’hypothèse que l’habitude d’associer dans l’enseignement des noms aux théorèmes ait été introduite à la fin du 19e siècle est aussi reprise dans un encart de manuel de 4ème sur lequel nous reviendrons :

Reportons-nous aux sources. La scolie de l'édition de 1883 du traité de Rouché et Comberousse donnée pour la première occurrence de cette appellation figure dans l'édition de 1868, vingt-cinq ans plus tôt (elle est bien en revanche absente des éditions antérieures de 1866 et de 1864) :
Dès la première édition, c'est-à-dire en 1864, le « théorème de Thalès » est néanmoins explicitement mentionné dans un autre paragraphe du même traité (paragraphe repris dans les éditions de 1866, §381, p. 229 et de 1868, § 366, p. 229 ) (cette occurrence est relevée dans http://euclides.fr/cahiers/2/thales/thales.pdf) :
La dénomination « théorème de Thalès » est donc utilisée dès les premières éditions du traité de Rouché et Comberousse, c’est-à-dire avant 1870. L'explication proposée, selon laquelle l’introduction de cette dénomination répondrait à une incitation faite aux agrégés de développer des connaissances en histoire apparue au début de la Troisième République, ne peut donc pas être retenue.
L'occurrence dans l'édition de 1864 n'est pas seulement antérieure à celle de 1883, souvent donnée pour la première : sa formulation indique qu'il ne s'agit pas pour l'auteur d'une désignation qu'il introduirait mais d'une désignation déjà reçue. Elle l’est en effet. Elle est par exemple déjà utilisée en 1853 par Auguste Comte :
Avec quelques pages plus loin la mention du « théorème de Thalès » :
Son emploi est attesté encore avant par Cournot en 1847 :
Et l'usage qu'en fait Cournot indique à nouveau que c'est aussi pour lui une expression reçue...
L'usage de l’appellation « théorème de Thalès » est donc déjà bien attesté dans la première moitié du 19e siècle. De toute évidence, l'édition de 1883 du Traité de géométrie élémentaire de Rouché et Comberousse n’en contient donc pas la première occurrence publiée. Ce traité pourrait néanmoins avoir joué un rôle dans la diffusion de cette appellation dans l'enseignement, mais la mention de l'occurrence dans ce traité ne suffit pas à l’établir.
Présenter le passage du traité de Rouché et Comberousse de 1883 comme contenant la première occurrence de l'appellation « théorème de Thalès » fait nécessairement forte impression. Cette assertion a de fait été souvent reprise. La valeur de cette citation tient à ce qu'elle contiendrait la première occurrence de cette appellation. Cela nous donne l'impression d'être devant un fait, d'être témoin de l'origine de quelque chose, d'assister à une naissance : on a une date de naissance, 1883, et un lieu de naissance, le Traité de géométrie élémentaire de Rouché et Comberousse. La conviction qu'il s'agit là de l'origine invite en outre à en chercher une explication. Ce sera ici le fait que «vers les débuts de la Troisième République, le programme de l'agrégation de mathématiques stipulait que les candidats devaient faire montre de connaissances en histoire de la discipline ». Qu'une telle injonction puisse se trouver dans un programme de l'agrégation de mathématiques est à la fois crédible et vérifiable. Mais cette explication est d'emblée en partie légitimée par l'impression de sa nécessité. Non pas la nécessité de cette explication, mais la nécessité d'une explication : il y a quelque chose à expliquer. La rigueur exige bien entendu que cette explication soit présentée comme une hypothèse, mais le fait d'avoir devant soi la première occurrence de cette appellation appelle une explication, cela rend une hypothèse nécessaire. L'hypothèse proposée n'est pas nécessaire, et elle est d'ailleurs explicitement introduite en tant qu'hypothèse (« Une hypothèse peut être avancée »), mais une hypothèse est nécessaire. L'hypothèse proposée répond à cette nécessité. Elle a de ce fait d'emblée un caractère satisfaisant : elle satisfait le besoin d'une justification qui naît du fait de cette première occurrence. Il serait possible d'objecter ici que dans aucune des citations données il n'est dit que l'occurrence de 1883 soit la première. C'est incontestable. Mais cela est néanmoins présupposé par le fait de mentionner cette occurrence et cela se manifeste en outre par la justification qui en est donnée (le programme d'agrégation...) : si cette occurrence n'était pas tenue pour sans précédent, pourquoi la mentionner et surtout pourquoi faudrait-il en donner une explication ? L'explication donnée vient rendre compte de l'apparition de cette appellation, ce qui présuppose qu'elle soit sans précédent. Cela rend inversement nécessaire une explication. L'explication donnée comble le besoin d'explication créé en creux et elle apparaît de ce fait satisfaisante. Elle peut être ostensiblement présentée comme une hypothèse, elle n'en aura pas moins le mérite de répondre au besoin d'explication ainsi créé. Mais la nécessité d'une explication repose sur un fait en réalité illusoire : que ce serait là la première occurrence. Les occurrences que nous avons données dans les éditions du Traité de géométrie élémentaire antérieures à 1883, ou celles de Comte et de Cournot, ne servent pas à remplacer une date et un lieu de naissance par d'autres ; elles n'ont pas été données pour établir un nouveau record. Elles servent au contraire à montrer que se prévaloir du caractère sans précédent d'une occurrence est périlleux : c'est aussi difficile à établir que facile à réfuter. Il s’agit avant tout d’en comprendre l'attrait. On retrouve ici l'attrait de l'origine, de la scène primitive. Il peut sembler constitutif de l'intérêt pour l'histoire, et plus particulièrement pour l'histoire des mathématiques : connaître l'histoire des mathématiques, ce serait connaître l'origine du théorème de Thalès, de l'appellation « théorème de Thalès », etc. C’est en outre comme une connaissance remarquablement facile à acquérir et à diffuser : une date et un nom. C'est de ce fait une forme de connaissance à bien des égards optimale : un effort minimal d'acquisition, qui ne suppose en particulier aucun effort de compréhension, pour un maximum d'effets. Son attrait et sa facilité d'acquisition en assurent un bon accueil et une large diffusion. Rares seront aussi les situations où elle pourra être discutée. Il y a là aussi un rapport au savoir propre à une forme d'amateurisme. L'amateur va en effet volontiers renoncer au contrôle de ses connaissances pour lequel il s’en remet au spécialiste. Admettre ce qu'on lui dit, surtout si c'est écrit, lui convient ; il ne peut de toute façon guère faire autrement. A défaut de constater que c’est la première occurrence, il a tout de même été possible de constater que c’en était une. Et si le fondement de la conviction d’avoir repéré l'origine est fragile, les conséquences escomptées le sont aussi, et pas seulement parce qu’elles partent d’un fait qui l’est. Savoir qu'un ouvrage serait le premier à faire quelque chose, ici à utiliser l'appellation « théorème de Thalès », ne suffit pas à établir qu'il soit à l'origine des usages subséquents : les mêmes raisons qui ont pu conduire Rouché et Comberousse à adopter cette désignation, ont aussi pu en conduire d'autres à le faire. On a pourtant vu l’intérêt de connaître les sources et on le verra encore. Mais leur intérêt n’est ni d’accéder à une hypothétique origine ni dans les connaissances que l’on pourrait en escompter, mais dans les différences entre ce que nous pouvons y lire et nos attentes et ce que celles-ci nous font découvrir sur nos préjugés induits par notre représentation actuelle des mathématiques. La recherche de la première occurrence de cette appellation remplace la quête d'une origine (l'origine du « théorème de Thalès »), par une autre (l'origine de l'appellation « théorème de Thalès »). La quête de l’origine n’a pas été abandonnée, elle a seulement été déplacée. Il importe de reconnaître la fragilité inhérente à cette recherche, aux dates et aux lieux donnés pour les premiers, qui fait naître le besoin d'une explication qu'il ne sera ensuite pas difficile de satisfaire.
L’usage des sources est en l’occurrence exactement inverse de celui que nous avons fait de celles du récit de la mesure de la pyramide par Thalès. Nous étions enclins à penser que le théorème de Thalès était nécessaire, nous avons pu découvrir qu’il ne l’était pas. Nous étions enclins à considérer comme allant de soi l’idée d’un Thalès apprenant les mathématiques aux Égyptiens, nous avons découvert que c’était plutôt l’inverse, etc. Ces sources nous ont servi à changer la compréhension que nous avions du récit donné dans l’encart. Elles nous ont fait découvrir ce que nous ne savions pas déjà et ce que nous ne pouvions bien souvent pas envisager sans elles. Ici, à quoi sert la source ? Elle sert fondamentalement à introduire l’idée que les dénominations sont un moyen d’introduire un peu d’histoire des mathématiques dans leur enseignement. Mais cette idée, nous l’avions déjà : c’est précisément l’idée que nous avons de l’intérêt de ces dénominations. Autrement dit, la source sert à conforter une idée que nous avons déjà ; elle ne nous fait rien découvrir sinon une date et un nom, deux en l’occurrence…, offrant une précision illusoire.
Le récit de l’encart du Nouveau Prisme peut à présent être comparé aux sources antiques conservées rapportant la mesure de la pyramide par Thalès.
L’encart reprend la référence au Pharaon Amasis qui ne se trouve que dans le récit de Plutarque. On y retrouve aussi la notion de proportion qui ne figure aussi que chez Plutarque. De même, la précision que le bâton doit être placé à la pointe de l’ombre de la pyramide ne figure que chez Plutarque. En revanche, la condition que la mesure soit effectuée au moment où « la longueur de tout objet égale la hauteur de l’objet » ne se trouve pas chez Plutarque, mais chez Pline et Diogène. La formulation, « la longueur de tout objet égale la hauteur de l’objet », l’apparente plutôt à celle de Pline. Que ce soit une personne qui joue le rôle du bâton se trouve en revanche dans le récit de Diogène Laërce. On peut retrouver cette condition dans le fragment de Pline mais à condition d’interpréter « corpori » par « corps » comme le fait Littré dans sa traduction, et en sous-entendant « corps humain », plutôt que par « objet » comme le fait Dumont dans la sienne.
Le récit du Nouveau Prisme apparaît comme une combinaison relativement complexe d'éléments des récits de Pline, de Plutarque et de Diogène Laërce. Des éléments qui ne figurent dans aucune de ces sources ont aussi été ajoutés et peuvent à présent être identifiés. Que ce soit l’ombre de Thalès lui-même qui soit considérée n'apparaît dans aucune de ces sources, pas plus que la référence à des aides ni le tracé d’un cercle sur le sable. Mais surtout, les sources n’indiquent aucune valeur : ni la date des jours auxquels il est possible de faire la mesure, ni la valeur de la hauteur de la pyramide calculée par Thalès.
Les sources anciennes ne sont guère précises sur le protocole exact de la mesure. Ce n’était sans doute pas leur propos compte tenu, comme nous l’avons vu, du genre des textes dont elles relèvent. Si cela permet ensuite d'y voir à sa guise l'application du « théorème de Thalès », cela oblige aussi les auteurs des encarts à compléter eux-mêmes la description du protocole de mesure. Examinons plus précisément le protocole proposé dans notre encart.
Suivant le protocole présenté dans l’encart du Nouveau Prisme, la mesure doit être effectuée au « bon moment ». Seulement deux jours dans l’année permettent cette mesure : le 21 novembre et le 20 janvier. Une parenthèse nous explique que ce sont les deux jours où le soleil est au zénith, c'est-à-dire à la verticale de l'observateur. La latitude du Caire étant d'environ 30° Nord, la hauteur maximale du Soleil varie entre les deux solstices de 60°-23°=37° à 60°+23°=83° (en prenant l'écliptique à 23°). Le Soleil n'est donc jamais au Zénith au Caire ! Et de toute façon, il n’y aurait alors pas d’ombre à midi ; la mesure de la pyramide serait donc impossible! La condition selon laquelle « la longueur de l’ombre de tout objet égale la hauteur de l’objet » est satisfaite quand le Soleil est à la hauteur de 45°. La hauteur maximale du Soleil variant au Caire entre 37° et 83°, cette hauteur est atteinte deux fois par jour presque tous les jours de l'année, et non seulement en deux jours particuliers. Encore faut-il s’assurer que l’extrémité de l’ombre soit bien à l’extérieur de la pyramide. Le résultat de la mesure effectuée par Thalès aurait donc été de 276 coudées. Une telle valeur ne peut être connue qu’à partir d’une source historique. Il convient de bien apprécier cette nécessité. Or, aucune source ne mentionne la valeur obtenue par Thalès. Ce nombre a donc nécessairement été inventé. Il ne peut même pas avoir été obtenu en suivant le protocole décrit qui s’avère en l’occurrence tout à fait fantaisiste. L’encart se termine en précisant que « depuis, d’autres méthodes ont permis de mesurer la hauteur réelle qui est de 280 coudées soit environ 147m ». La différence étant relativement petite, nous sommes conduits à considérer, avec un peu de condescendance, que ce n’est pas si mal pour l’époque… Autrement dit, l’encart nous propose là une belle illustration du caractère remarquable de la science grecque en même temps que du progrès des sciences qui nous permet de connaître aujourd’hui la hauteur réelle.
Comme non seulement le protocole, mais aussi la valeur attribuée à Thalès, sont en fait entièrement fictifs, la grandeur de la science grecque et de la supériorité de la nôtre le sont en l’occurrence aussi. Sans doute la science grecque est elle remarquable, et sans doute la science actuelle lui est supérieure, mais ni l’un ni l’autre ne sont ici établis ; le protocole et les valeurs choisies ne font que conforter ces préjugés. Si l'encart présuppose la supériorité de la science actuelle, il ne l’illustre nullement. En effet, il n’est pas expliqué comment les dates du 21 novembre et du 20 janvier ont été calculées. Les élèves n’ont donc pas les moyens de les déterminer eux-mêmes. Ils ne peuvent donc avoir qu’une compréhension confuse de ce protocole. Cela d’autant plus que la justification donnée pour ces dates est doublement absurde : le Soleil n’est jamais au zénith au Caire et cette position ne permet pas d’effectuer la mesure voulue. Les nombreuses précisions données ont un caractère savant mais ne servent qu’à produire des effets de précision dans un protocole factice. Les élèves ont ainsi le sentiment de savoir mesurer la hauteur de la pyramide, mais n’en ont en fait aucun savoir effectif. C’est un simulacre de précision aussi bien historique que mathématique qui leur est présenté. La science actuelle est évoquée au travers « d’autres méthodes » permettant de mesurer « la hauteur réelle », mais aucune indication n’est donnée à propos de ces méthodes. Ainsi, Thalès obtiendrait une bonne approximation, quand nous connaîtrions « la hauteur réelle ». La condescendance historique se double ici d’une erreur épistémologique manifeste : la mesure réalisée aujourd’hui n’est pas plus la hauteur réelle que celle que Thalès aurait pu obtenir. Elle peut être plus fiable et plus précise, ces deux critères ayant eux-mêmes besoin d’être clarifiés, mais elle n’est ni plus ni moins réelle que celle que Thalès aurait pu effectuer. Mais peut-être l’introduction de cet adjectif dans la dernière phrase de l’encart répond-elle au sentiment confus de l’auteur que tout ce qui précède est bien imaginaire.
Les dates du 21 novembre et du 20 janvier associées à la hauteur de 276 coudées restent mystérieuses. Elles se retrouvent néanmoins dans d’autres sources. Ces deux dates sont par exemple mentionnées par le site euclides.fr :

Si les dates du 21 novembre et du 20 janvier sont bien reprises, elle ne désignent plus néanmoins les jours où le Soleil serait au zénith, mais ceux où il serait à la hauteur de 45° à midi. Les deux dates ne changent pas, mais leur caractérisation si. Il n’y a bien alors que deux jours dans l’année où le Soleil est au Caire à midi à la hauteur de 45°, mais aucune raison n’est donnée justifiant de fixer l’heure de la mesure à midi. Rappelons toutefois que Pline, l’auteur le plus ancien relatant cette mesure, évoque une heure précise (« il mesura l'ombre à l'heure où elle est égale aux corps »), mais sans avoir besoin de préciser des jours particuliers.
On retrouve dans la même page la hauteur de 276 coudées comme valeur obtenue par Thalès :

Les mêmes valeurs se retrouvent sur le site de l’irem de la Réunion :
La mention du 21 novembre et du 20 janvier n’apparaît pas cette fois. Mais à partir de la même mesure, soit 18 thalès, et du même résultat exprimé en coudées, soit 276, 25 coudées, Thalès arrive cette fois à la bonne valeur (« la valeur réelle »!) exprimée en mètres, soit 147 m, alors qu’il fallait dans l’encart du Nouveau Prisme pour arriver à cette valeur 280 coudées. Il suffit d’adapter la conversion des coudées en mètres pour que Thalès obtienne la « bonne » valeur.... C’est tout aussi fantaisiste, mais un peu moins condescendant.
On retrouve en revanche la mention du 21 novembre et du 20 janvier, avec les mêmes valeurs, sur le site de mathématiques du lycée Saint-Louis :

Cette fois, la conversion des coudées en mètres n’a pas été choisie de manière à attribuer à Thalès la « bonne » mesure. La condescendance est aussi plus explicite : « Comme quoi, la mesure de Thalès était déjà passablement précise ».
Une partie de ces valeurs se retrouvent dans l’encart consacré à Thalès dans le Magnard, Zenius, de 4ème :

La valeur du côté de la pyramide est à nouveau de 134 et le résultat de la mesure attribuée à Thalès 18, l’unité de longueur étant encore la taille de Thalès, considérée connue et valant 1,71m (le site de l’Irem de la Réunion lui attribuait une taille de 1,73m).
Les mêmes valeurs, sans les dates, se retrouvent dans le Phare, 4°, de Hachette, avec à nouveau la taille de Thalès évaluée à 1,73 m :

On retrouve encore les dates du 21 novembre et du 20 janvier associées à la hauteur de 276 coudées dans le passage consacré au « théorème de Thalès » dans le livre Le Théorème du perroquet de Denis Guedj :

La formulation de la condition que « l’ombre soit égale à l’objet » est très semblable à la traduction de Pline donnée par Jean-Paul Dumont qui évoquait aussi l’égalité « à son objet », par opposition à celle de Littré dans laquelle il est question de l’égalité « aux corps », plus proche du texte latin. On retrouve surtout bien les deux mêmes dates avec des justifications encore différentes. Il s’agit cette fois de faire en sorte que l’ombre du Soleil soit perpendiculaire à l’un des côtés de la base de la pyramide. Cette disposition était en effet supposée dans l’encart et les textes précédents, sans que l’on sache comment elle était satisfaite. L’application Google Earth permet à chacun de vérifier facilement l’orientation de Kheops et de constater que ses quatre côtés, comme ceux des deux autres pyramides, indiquent bien en effet les quatre points cardinaux :
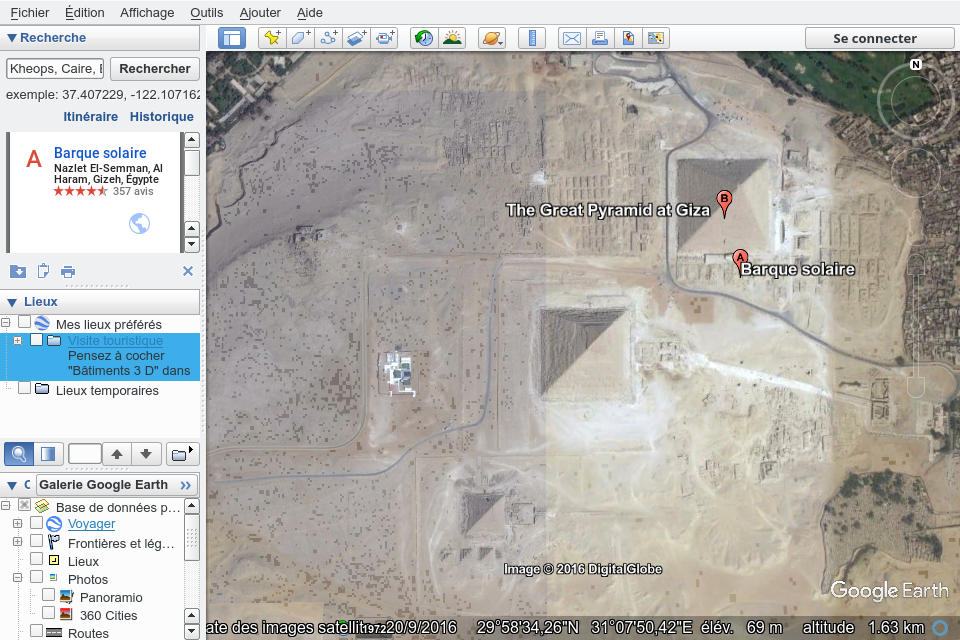
Le méridien du lieu est donc de ce fait perpendiculaire à la base. A midi, l’ombre du Soleil est de ce fait chaque jour perpendiculaire à la base. L’heure, midi, est ainsi choisie afin d’avoir une ombre perpendiculaire à la base. C’est donc l’orientation particulière des pyramides du Caire qui justifie que l’heure retenue soit midi. Ce protocole ne permet pas la mesure de la hauteur d’une pyramide sans en connaître l’orientation. Le jour est quant à lui choisi pour que le Soleil soit à midi à la hauteur de 45°.
Remarquons néanmoins qu’il n’est pas nécessaire que l’ombre soit perpendiculaire à la base de la pyramide.
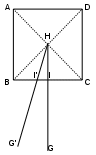
Le même raisonnement permet de déterminer le point $G’$ (voir figure), pointe de l’ombre de la pyramide, tel que $G’H$ soit égal à la hauteur de la pyramide (ainsi que $GH$). Le côté $HI’$ est l’hypoténuse du triangle $HII’$ dont les deux autres côtés $HI$ et $II’$ peuvent être déterminés une fois la position de $G’$ connue. Cela dispense du calcul des deux dates et permet surtout de faire la mesure à peu près n’importe quel jour de l’année, et indépendamment de l’orientation des pyramides, à tout moment de la journée où le Soleil est à la hauteur de 45°.
Les précisions données dans ce protocole permettent bien néanmoins, contrairement aux précédents, d’effectuer la mesure voulue. Le calcul des deux jours de l’année où le Soleil est à midi, au Caire, à la hauteur de 45° n’est pas donné. Mais il est indiqué que ces deux dates ont été données par « les astronomes ». Il est ainsi au moins explicite que leur détermination suppose un calcul qui n’est pas donné ; nous savons ainsi que nous devons en admettre le résultat. Cela fait néanmoins dépendre la mesure de la hauteur d’une pyramide d’un modèle, ou à défaut d’une table, de la position apparente annuelle du Soleil et ne s’applique qu’à des pyramides orientées comme celles du Caire. Réaliser cette mesure devient plus compliqué qu’il ne semblait...
Considérons à présent la mesure effectuée et la hauteur calculée à partir d’elle. La suite de ce passage mentionne les mêmes valeurs que dans l’encart du Nouveau Prisme :

La similitude non seulement des valeurs mais aussi des textes cités avec celui-ci est flagrante. Elle ne peut être due au hasard. Mais le dernier paragraphe n’est lui repris dans aucun des texte cités. Il est pourtant intéressant : « M. Ruche ne leur dit pas le temps qu’il avait passé, la nuit précédente, pour effectuer tous ces calculs. Combien de fois il s’était trompé ! ». Ainsi, tous ces calculs sont présentés comme étant ceux de M. Ruche, alias Denis Guedj ! L’unité de mesure, le thalès, est évidemment fantaisiste, mais surtout il est manifeste que les 18 thalès ne sont pas le résultat d’une quelconque mesure effectuée par M. Ruche, Denis Guedj, et moins encore par Thalès, mais celui d’un calcul effectué (de nuit…, et plus probablement à Paris qu’au Caire) à partir de la hauteur de la pyramide afin d’en déterminer une mesure fictive plausible, et non l’inverse. Le texte de Denis Guedj est là encore plus cohérent, rigoureux et complet ; il est le seul qui assume et rend explicite son caractère imaginaire. Sa cohérence et surtout l’indication explicite de son caractère imaginaire en font une source probable des textes moins cohérents dans lesquels les deux mêmes dates et les mêmes valeurs sont reprises sans que ne soit indiqué la manière dont elles ont été obtenues, ni surtout leur caractère entièrement fictif.
Ces deux dates, le 21 novembre et le 20 janvier, ne pouvaient guère provenir d’un calcul effectué par Thalès. Nous savons qu’elles ne figurent dans aucune des sources antiques connues rapportant cette mesure où elles devraient se trouver. Il y a aussi le calcul et les connaissances astronomiques que leur détermination suppose. Mais en apprécier la possibilité à l’époque de Thalès supposerait néanmoins un débat érudit. Il est en revanche évident que ces dates ne sont pas données dans un calendrier égyptien ou grec. Or, cela est pour le moins étrange… Le protocole est de ce fait décrit avec un mélange de mesures exprimées en coudées, puis converties en mètres, et de ces deux dates données, elles, exclusivement dans notre calendrier, sans conversion : les astronomes consultés par .M. Ruche n’étaient de toute évidence pas contemporains de Thalès… Si les mesures étaient authentiques, comme leur conversion en coudées essaye de nous le faire croire (on se souvient que le paragraphe de Pline rapportant la mesure de la pyramide donne aussi la profondeur d’un puits exprimée en coudées), les deux dates auraient aussi dû être exprimées dans un système de l’époque pour être ensuite converties dans le nôtre. Mais s’il est facile de proposer un simulacre de conversion en coudées de valeurs considérées en mètres et de leur conférer ainsi un semblant d’authenticité historique, il est autrement plus difficile de le faire pour des dates : cela supposerait la présentation d’un autre calendrier puis une conversion dans celui-ci des dates calculées dans le nôtre, conversion que l’irrégularité du mouvement du Soleil, qui intervient aussi bien dans les dates à calculer que dans leur conversion, rendrait autrement plus compliquée que l’application du « théorème de Thalès » qu’il s’agit de mettre en scène. Le problème posé par le calendrier n’a ni pu être traité par un subterfuge comme ont pu l’être les longueurs données en coudées ni être admis comme l’a été le calcul des deux jours. Le calendrier dans lequel les deux dates sont exprimées est l’indice le plus sûr de l’inauthenticité de cette mesure.
Bien que très semblables à celui de Denis Guedj, les extraits cités omettent tous d’indiquer l’orientation des pyramides, pourtant essentielle à son calcul. La reprise de l’heure, midi, perd alors tout son sens (assurer la perpendicularité de l’ombre à la base de la pyramide) et des justifications fantaisistes lui sont substituées, comme dans l’encart du Nouveau Prisme où ce serait l’heure à laquelle le Soleil serait au zénith. L’encart du Zénius et le site de l’Irem de la Réunion n’indiquent quant à eux ni le jour ni l’heure qui garantissent la perpendicularité de l’ombre à la base de la pyramide qu’ils supposent pourtant dans leur calcul. Tous ces textes reprennent donc un calcul sans en restituer correctement les conditions ; il ne s’agit de toute évidence que d’appliquer le théorème de Thalès sans s’assurer de l’effectivité du protocole proposé.
L’encart du Zénius attribue à Thalès une taille de 1,71m quand le site de l’Irem de la Réunion et le Phare 4° lui en attribuent une de 1,73m. Pourquoi cette différence ? Elle s’explique par le fait que l’Irem de la Réunion et le Phare 4 ont choisi la taille de Thalès pour que celui-ci obtienne au terme du même calcul la bonne hauteur. L’encart du Zénius lui attribue en revanche la valeur approchée adoptée par Denis Guedj. Cela permet ensuite de s’extasier sur la faiblesse de la différence. Ainsi, la variation de la taille de Thalès reflète un parti pris sur la possibilité que Thalès ait obtenu la « bonne » hauteur ; elle est fonction de la condescendance de ces récits. Car bien entendu, comme rien de tout cela n’est dans les sources, la coïncidence ou non de la mesure obtenue par Thalès avec la « bonne » est entièrement laissée au choix des auteurs des encarts. Elle est donc exclusivement le produit et la manifestation de leur conception du rapport de la science actuelle à la science passée. Elle ne nous apprend rien sur Thalès et la science de son époque, mais beaucoup sur la conception que les auteurs actuels des manuels ont des sciences et de leur histoire, et en particulier de leur progrès. De la même manière, l’auteur du site Mathématiques au lycée français Saint-Louis s’est plu quant à lui à ajouter une touche personnelle en indiquant que pour récompenser Thalès, « les prêtres lui donnèrent accès à la bibliothèque où il put consulter de nombreux ouvrages d’astronomie ». A nouveau, la connaissance des sources nous permet de savoir qu’il s’agit là d’un ajout. Cette précision en apparence anodine a néanmoins aussi de quoi surprendre. Voici par exemple ce qu’écrit Otto Neugebauer, spécialiste d’astronomie antique, au début de la partie qu’il consacre à l’astronomie mathématique égyptienne dans son A History of Ancient Mathematical Astronomy :
L’Égypte n’a pas sa place dans un travail consacré à l’histoire de l’astronomie mathématique. Néanmoins, j’ai consacré un « livre » à ce sujet afin d’attirer l’attention du lecteur sur son insignifiance qui ne saurait être trop soulignée en comparaison des contributions babyloniennes et grecques au développement de l’astronomie scientifique.
Les très rares manuscrits égyptiens qui nous sont parvenus et contenant des mathématiques ne traitent pas d’astronomie. L’auteur du site Mathématiques au lycée français Saint-Louis attribue subrepticement aux égyptiens une production de livres en astronomie que rien n’atteste. Ce faisant, il ne fait que projeter sur eux la conception qu’il se fait des modalités d’acquisition des connaissances et en particulier du rôle des livres dans celle-ci sans en vérifier le bien fondé.
L’encart du Nouveau Prisme apparaît encore plus clairement à présent être le résultat d’une succession de dé/ré-contextualisations de textes de genres très différents présentant comme un fait historique une restitution erronée d’un calcul et de valeurs fictifs que l’on retrouve dans un roman contemporain inspirés de divers récits antiques eux-mêmes très postérieurs à l’époque de Thalès. Peut-être le « théorème de Thalès » pourrait-il être appelé le « théorème du perroquet » afin de rappeler le rôle éventuel de ce roman dans de nombreuses présentations du récit qui en relate l’origine et surtout pour rappeler le risque qu’il y a à répéter des arguments aussi bien historiques que mathématiques sans en contrôler les sources et le bien fondé.
Le passage du Théorème du perroquet rapportant la mesure de la pyramide par Thalès est une source possible des encarts dans lesquels les mêmes valeurs se retrouvent. L’étude des sources conservées permet d’établir que les valeurs utilisées et calculées ne s’y trouvent pas. Comme, par ailleurs, il n’en existe aucune justification intrinsèque, les encarts dans lesquels elles figurent ne peuvent les avoir introduites indépendamment les uns des autres. Les précisions qui y sont données sont inauthentiques sans pour autant décrire un protocole de mesure effectif. Elles ne font guère que produire des effets de précision. Ces encarts proposent un protocole de mesure aussi fictifs que le récit qu’ils donnent de son origine. Le manque de rigueur mathématique et historique vont en l’occurrence ici de paire.
Si les éléments dégagés à partir du Nouveau Prisme de Belin se retrouvent dans la plupart des encarts historiques consacrés au « théorème de Thalès », certains encarts sont un peu plus sophistiqués et marquent une certaine distance critique.
L’encart du Zénius, 4ème, de Magnard ne reprend pas certains des préjugés communs au Nouveau Prisme et à de nombreux autres :

Cet encart précise que le récit concernant Thalès est rapporté (« on rapporte »), et ce faisant jette un certain doute sur son authenticité, en ne donnant toujours aucune source. Mais surtout, il inverse complètement le sens de la transmission entre la Grèce et l’Égypte : Thalès est présenté comme ayant « appri[s] à mesurer la distance séparant un navire en mer de la côte ». Le deuxième paragraphe est encore plus explicite : « la propriété que nous appelons aujourd’hui le théorème de Thalès était donc déjà utilisée et n’a pas été découverte par Thalès lui-même ». Une affirmation semblable se trouve dans l'article de Wikipedia consacré à Thalès :
Cependant, aucun texte ancien n'attribue la découverte du théorème à Thalès. Dans son commentaire sur les Éléments d'Euclide, Proclos affirme que Thalès aurait rapporté le résultat de son voyage en Égypte. Hérodote rapporte la même chose et précise qu'il est l'un des sept sages fondateurs de cette civilisation.
Mais si les sources indiquent bien que Thalès a plutôt appris la géométrie des Égyptiens, rien ne permet en revanche d’affirmer qu’ils lui auraient appris à mesurer la distance d’un navire à la côte. Proclus, citant Eudème, attribue au contraire explicitement à Thalès cette mesure. En outre, suivant Eudème, le théorème utilisé pour cela n’était justement pas le « théorème de Thalès » ! Quant à Hérodote, et nous avons cité intégralement le passage de son Enquête se rapportant à la géométrie, ni dans ce passage, ni ailleurs, il ne « rapporte la même chose ». Cet encart continue donc de présupposer que cette mesure nécessite le « théorème de Thalès » et sur cette base en attribue l'origine aux Égyptiens. Ainsi, l’attribution du « théorème de Thalès » à Thalès est remise en cause, mais le présupposé selon lequel il serait ici nécessaire demeure, ce qui permet d'en attribuer à présent la découverte aux Égyptiens. Le ressort est le même, seul change le destinataire.
De fait, la démarche critique mise en œuvre dans cet encart n'a pas permis à son auteur d’en découvrir le présupposé sur lequel son raisonnement est fondé. Il lui suffisait pourtant de se reporter à Proclus, la seule source rapportant cette mesure. En conséquence, au lieu de découvrir ce présupposé, la correction qu’il introduit (la diffusion des connaissances allait plutôt de l'Égypte vers la Grèce que dans le sens inverse) lui fait en étendre la portée : le théorème n’aurait pas été seulement utilisé par Thalès mais déjà, pour la même raison, par les Égyptiens. L'association du « théorème de Thalès » à ces mesures n'est pas corrigée mais au contraire renforcée et étendue.
Cet encart peut être pris comme un avertissement. Il manifeste en effet une certaine bonne volonté historique : il exploite des données historiques qui ne sont pas celles reprises un peu partout ; il ne fait preuve d'aucune condescendance ; il propose un raisonnement propre ; sa conclusion remet en cause à la fois le bien fondé de l'appellation « théorème de Thalès » adoptée dans le manuel dont il est issu et l'origine exclusivement grecque des mathématiques. Cette liste conséquente est en accord avec ce que nous avons pu présenter. Son raisonnement partage pourtant encore avec les autres encarts un de leurs principaux préjugés erronés, ce qui le rend incontestablement faux. S'il se démarque d’une certaine idéologie commune, il n'a pas pour autant réussi à se soustraire au présupposé que la mesure ne pouvait être obtenue qu'en appliquant le « théorème de Thalès ». La bonne volonté historique n'est manifestement pas suffisante : disposer de quelques connaissances historiques peut malgré tout encore conduire à renforcer et à étendre notre représentation scolaire des mathématiques. L'auteur de cet encart ne s'est pas détaché de sa représentation du « théorème de Thalès » : c'est elle qui est à l'œuvre, c'est elle qu'il prête à Thalès ; il ne fait que l'étendre aux Égyptiens. N'ayant visiblement pas lu Thalès, et pour cause..., ni aucun manuscrit égyptien montrant une quelconque application du « théorème de Thalès », qu'il n'hésite pourtant pas à leur attribuer, ni aucune autre source, il n'avait aucun moyen de changer sa représentation de l’usage de ce théorème. Sans lecture des sources, nous ne pouvons sortir de notre représentation scolaire, nous ne disposons d'aucune alternative et nous ne pouvons que diffuser subrepticement cette représentation. La lecture de la seule source disponible sur la mesure par Thalès de la distance d'un navire au rivage nous donne à l'inverse l'occasion de découvrir que cette mesure n'est pas nécessairement associée au « théorème de Thalès », et que, d’après Proclus, Eudème l’associait à un autre théorème, en l’occurrence un théorème d'égalité des triangles. Cela nous semblera la première fois d'abord étrange, à la fois incompréhensible et sans doute aussi décevant : ce n'est pas ce que l'on attendait, on ne peut plus exploiter cette histoire pour son cours comme on l’envisageait... Mais si au lieu de passer outre on s'y arrête, on aura justement découvert quelque chose d'inattendu : au lieu de conforter et de propager indûment notre représentation des mathématiques nous sommes alors en mesure d'en découvrir certains partis pris, autrement trop familiers pour être perçus. A l'inverse, rien d'inattendu ne pourra jamais arriver sans la lecture d'aucune source. L'enseignement de cet encart est ainsi double : l'acquisition d'éléments d'histoire des mathématiques extérieurs ne suffit pas à nous sortir de notre représentation scolaire des mathématiques et peut au contraire la renforcer et la propager ; la lecture d'autres sources est nécessaire pour sortir de cette représentation et pour en découvrir les caractéristiques.
Considérons un autre encart, déjà cité, qui se démarque aussi des autres en ne se contentant pas de rapporter sans examen critique le récit de l'usage du « théorème de Thalès » par Thalès.

Le titre de l'encart annonce d’emblée qu’il y est question du nom du théorème et non plus de l'origine de celui-ci pour en justifier le nom. La carte placée au bas de l'encart, introduite par le dernier paragraphe du texte situé au-dessus, illustre le fait que l'appellation « théorème de Thalès » peut désigner des théorèmes différents selon les pays, en l’occurrence européens. Rien ne suggérant qu'un choix serait plus pertinent qu’un autre, et en particulier celui adopté en France, celui-ci n'apparaît plus dès lors aller de soi. Sans avoir besoin de recourir à l’histoire, la diversité des appellations adoptées selon les pays permet aussi de remettre en cause l’évidence de notre appellation.
Mais cet encart ne s'en tient pas à cela. Comme le précédent (Zénius, 4e, 2011, p. 214), il attribue la découverte du « théorème de Thalès » aux Égyptiens. Il ne s'agit donc pas seulement de faire valoir la possibilité d'attribuer ce nom à d'autres théorèmes, il s'agit aussi en l'occurrence d'indiquer que le choix adopté en France est erroné :
Dans le papyrus de Rhind, il existe même une version de « son » théorème bien antérieure à son époque.
L’attribution du théorème aux Égyptiens n'est pas cette fois fondée sur l'allusion à un témoignage grec selon lequel « Thalès apprit à mesurer la distance séparant un navire en mer de la côte » (Zénius, 4e, 2011, p. 214) mais par la référence à un manuscrit égyptien : le papyrus de Rhind. Une source est cette fois citée. Il est même précisé que ce manuscrit « aurait été recopié vers 1650 avant J.-C. par le scribe Ahmès ». Tout cela est manifestement précis et savant : le manuscrit n'est lui-même qu'une copie d'un manuscrit, la date de cette copie et même le nom du copiste sont indiqués. Tout cela donné en légende d'une reproduction d’un extrait du papyrus dans lequel on distingue deux triangles avec, pour celui du bas, deux lignes verticales tracées à l'intérieur. On y reconnaît bien sûr la figure géométrique caractéristique du « théorème de Thalès ». La vérité semble ainsi rétablie : le « théorème de Thalès » n'est pas de Thalès comme chacun peut le constater en reconnaissant dans le papyrus de Rhind la figure caractéristique de ce théorème :

Le même extrait de ce papyrus est reproduit dans l'article de Wikipedia consacré au « théorème de Thalès » afin aussi d’établir que ce théorème était déjà connu en Égypte :

La légende placée sous la reproduction de l'extrait du papyrus est aussi explicite :
Le papyrus Rhind contient un équivalent du théorème de Thalès.
Le dernier paragraphe de l'article de Wikipedia renvoie à ce sujet à l'étude proposée dans le livre Mathématiques égyptiennes. Recherches sur les connaissances mathématiques de l'Égypte pharaonique de Sylvia Couchoud (Editions du Léopard d'or, 1993). Lisons donc cette étude, c’est-à-dire à la fois la transcription, la traduction et le commentaire qu'elle propose de ce problème, c’est-à-dire du problème 53 du papyrus de Rhind.
Voici reproduite l’intégralité du passage consacré dans ce livre à ce problème :
Il suffit de parcourir cet extrait pour constater qu’il n’y est nulle part question du théorème de Thalès ! La transcription, pour autant que l’on puisse en juger..., mais surtout la traduction, l’interprétation qui lui est associée, et son commentaire ne font pas intervenir ce théorème. Qu’en est-il donc de cette figure dans laquelle nous avions volontiers reconnu le « théorème de Thalès » et qui sert à en établir l’usage par les Égyptiens ?
Le problème 53 dont cette figure fait partie n’est pas n’importe quel problème : c’est sans doute l’un de ceux du papyrus de Rhind dont l’interprétation est la plus difficile et la plus controversée. Sylvia Couchoud commence d’ailleurs par indiquer que ce problème présente des difficultés d'interprétation particulières. Elle cite deux historiens, Peet, auteur d'une édition du manuscrit, et Neugebauer, autre spécialiste, déjà cité, de l'histoire des mathématiques antiques, qui jugent pour l'un que « le calcul n'a pas de sens » et pour l'autre qu'il y a une contradiction. Depuis, d’autres spécialistes en ont proposé d’autres interprétations. Les raisons de ces difficultés sont au moins faciles à déterminer, sinon à lever. L’énoncé de ce problème manque : on ne sait ni ce qui est cherché ni la signification des nombres considérés ni celles des calculs qui leur sont appliqués. Par ailleurs, la résolution donnée comprend à la fois des approximations (volontaires et habituelles) et des erreurs de calcul ou/et de copie (involontaires et habituelles). La figure que nous considérons est donc associée à un problème dont on ne sait pas ce qu’il calcule, ni à partir de quoi, ni comment, et qui comprend en outre des approximations, des erreurs de calcul ou/et de copie. Et bien sûr, aucun autre problème semblable ne nous est parvenu auquel la procédure ou la figure pourraient être comparés. Déterminer où commence et où fini ce problème est aussi matière à interprétation. Le manuscrit reproduit dans l'encart fait en effet clairement apparaître des lignes séparant les problèmes.
Mais Eisenlohr, à qui l'on doit la première édition et la première traduction (en allemand) de ce manuscrit, a aussi dû décider à cette occasion d’un découpage et d’une numérotation des problèmes. Il a considéré qu'il y avait là deux problèmes et non un seul. Il leur a par ailleurs attribué les numéros 53 et 54 alors que le sens de l'écriture étant de droite à gauche aurait plutôt dû conduire à l'ordre inverse.

|

|
| Problème 53 | Problème 54 |
Mais revenons à la figure sur laquelle l’encart de manuel comme la page du Wikipedia se fondent exclusivement. Pour y reconnaître le « théorème de Thalès », il faut au moins s’assurer que la valeur et la disposition des nombres dans la figure correspondent à une des configurations possibles de ce théorème. Examinons ce qu’il en est.
Grossissons pour cela un peu l'image :

La reproduction proposée sur le site du British Museum où est conservé le manuscrit n'est guère lisible :
Il n'est néanmoins pas difficile d’en trouver de meilleures reproductions :
Dont on peut en extraire la figure qui nous intéresse :
Il ne reste plus à présent qu’à la déchiffrer...
Nous pouvons nous aider pour cela de la transcription et de la traduction de Sylvia Couchoud. Afin néanmoins de pouvoir contrôler sa traduction de la figure, nous nous aiderons des deux tables du livre de Gillings donnant la transcription de nombres et de fractions en hiératique provenant de différents manuscrits égyptiens. Il nous suffit d’avoir ces transcriptions pour les nombres de 1 à 10 et pour les fractions, $\frac{1}{2}$, $\frac{1}{3}$, jusqu'à $\frac{1}{10}$ :

|

|
| Les dix premiers nombres | Les dix premières fractions |
Commençons par la transcription des inscriptions de la figure :

|
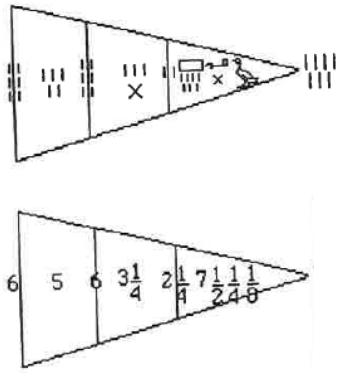
|
| Papyrus de Rhind |
Transcription et traduction Couchoud 1993, p. 60 |
On peut commencer par observer que le sens de la transcription a été inversé par rapport à l'original. Cela sans doute pour le rendre conforme à notre sens de lecture. Parcourons de droite à gauche les inscriptions de la figure originale, que nous avons numérotées de a à g, et comparons-les à leur transcription et à leur traduction.
On distingue sept ou huit inscriptions, toutes à l’encre rouge à l’exception d’une ou deux à l’encre noire. Les six traits rouge de la première inscription qui chevauchent la base du triangle ont été exactement reproduits et traduits par 6. L'inscription b suivante, celle à l’encre noire, a en revanche été remplacée par cinq traits. Cela ne correspond pas à la figure originale. C’est qu’il ne s’agit pas en fait d’une simple retranscription mais de la transcription en hiéroglyphes d'une inscription en hiératique. Ces cinq traits ont été traduits par 5, ce qui correspond bien à la valeur donnée par Gillings pour l'inscription hiératique originale. La différence de couleur n’a en revanche pas été restituée. La troisième inscription, c, six traits rouge qui chevauchent la deuxième ligne verticale, a à nouveau été transcrite par six traits et traduite par 6. La quatrième inscription, d, trois traits rouge au-dessus d'une croix rouge, placée entre les deux lignes qui divisent le triangle, a été exactement reproduite. Cette inscription a été traduite par un $3$ juxtaposé à $\frac{1}{4}$, c'est-à-dire $3 + \frac{1}{4}$, conformément à la valeur donnée par Gillings pour la croix dans l'écriture hiératique. La cinquième inscription, e, les deux traits au-dessus d'une croix rouge qui chevauchent la troisième ligne verticale, a été reproduite dans la traduction en hiéroglyphe sans la croix. La valeur donnée dans la traduction correspond bien néanmoins à celle de l'inscription originale, c'est-à-dire $2 \frac{1}{4}$. La croix manquante dans la transcription est sans doute simplement un oubli de l’auteur lors de la composition de la figure ; les scribes égyptiens ne sont pas les seuls à faire des erreurs de copie ! La sixième inscription (f et f') est plus difficile à déchiffrer. Il faut d’abord déterminer s'il y a là une seule inscription composée de quatre expressions (f avec f'), deux inscriptions distinctes (f d'une part, f' d'autre part) ou même une seule expression formée uniquement de trois expressions (f seule), l'inscription f' n'apparaissant pas sur toutes les reproductions :

Dans la traduction de Sylvia Couchoud, les inscriptions f et f' ont été rendues par un seul nombre composé de quatre expressions $7 \frac{1}{2} \frac{1}{4} \frac{1}{8}$. On peut se reporter ici à la transcription en hiératique de ce problème dans l’édition de Chace & alii 1929 sur laquelle sont fondées ces traductions pour essayer de déterminer s'il faut distinguer une ou deux inscriptions :
(d’après
la reproduction donnée dans Clagett 1999, p. 363)
Dans cette transcription, les inscriptions f et f' ne forment qu'une seule inscription composée de quatre expressions. Qu'elle soit écrite en hiératique n'empêche pas qu'il s'agit aussi d'une transcription, exactement comme c’était le cas des fragments grecs et latins édités par Diels ; ce n'est pas une image du manuscrit, mais une transcription faite au début du 20ème siècle, ce qui implique aussi un ensemble d'interprétations. On peut néanmoins y reconnaître les inscriptions f et f' dans le résultat final du dernier calcul :
(d’après
la reproduction donnée dans Clagett 1999, p. 363)
On peut de la même manière se reporter à la transcription en hiéroglyphes et à la traduction données par Sylvia Couchoud de cette dernière ligne de calcul :
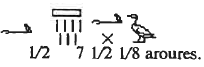
Mais au lieu de la valeur $7 \frac{1}{2} \frac{1}{4} \frac{1}{8}$ on trouve la valeur $7 \frac{1}{2} \frac{1}{8}$. Cependant, si on se reporte à la transcription en hiéroglyphe, on peut constater la présence de la croix, correspondant à notre $\frac{1}{4}$. La fraction $\frac{1}{4}$ a visiblement simplement été oubliée de la traduction ; il s'agit donc bien seulement d'une nouvelle erreur de copie (qui n'est d'ailleurs pas reproduite dans le commentaire), et c'est bien $7 \frac{1}{2} \frac{1}{4} \frac{1}{8}$ qu'il faut lire. Mais, compte tenu de cette erreur, si l'on s'était reporté uniquement à la traduction donnée par Sylvia Couchoud nous n'y aurions pas trouvé la confirmation de la présence du nombre $7 \frac{1}{2} \frac{1}{4} \frac{1}{8}$. Cela étant, la valeur traduite est-elle correcte ?
On reconnaît bien une croix, correspondant à $ \frac{1}{4}$, dans la transcription hiératique. Mais l’identification des trois autres expressions est moins évidente... En revanche, on reconnaît facilement dans la dernière inscription, g, située sous la pointe du triangle, l’expression en hiératique du 7, dont on peut ainsi vérifier la transcription et la traduction qui en ont été données. Mais la traduction ne comprend qu’un seul 7 quand la transcription en hiéroglyphe en comprend deux ! Il s'agit sans doute à nouveau d'un oubli dans la traduction. Mais on ne trouve pas pour autant deux expressions hiératiques identiques du 7 dans la reproduction de la figure originale : que l'inscription g soit un 7 ne fait guère de doute, mais elle est aussi clairement différente de f', qui ne figure pas dans les transcriptions données par Gillings, et qui est pourtant aussi traduite par 7 :
|
|
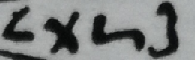
|
||||||||||||||||
|
|
Deux expressions différentes du texte en hiératique sont ainsi traduites par le même nombre : 7. Il s'agit-là sans doute à nouveau d'une erreur... Non ! L'expression f' correspond bien en fait à un 7, mais il s'agit d'un 7 mesurant une surface, appelée aroure dans la traduction de Couchoud, et dans d'autres setjat. Les deux 7 de la traduction désignent donc des grandeurs de natures différentes : l'un est une longueur, l'autre une surface. Ainsi, non seulement la position dans la figure de l'inscription f f' suggère qu'elle est associée à l'intérieur du triangle, mais surtout les expressions en hiératique utilisées le confirment. C'est pour la même raison que nous ne trouvions pas dans le tableau des fractions extrait de Gillings les expressions de f correspondant à $\frac{1}{2}$ et $\frac{1}{8}$ : leurs expressions ne sont pas les mêmes pour des longueurs et des surfaces. Et si nous avons d'abord cru reconnaître au milieu de l'inscription f la croix correspond à la fraction $\frac{1}{4}$, c'est seulement parce que dans ce cas particulier les expressions pour les surfaces exprimées en aroures et celles pour les longueurs coïncident. Cela n'en était pas moins une complète erreur d'interprétation qui nous a donnés l'impression, et la satisfaction, d'avoir une confirmation de la traduction par $\frac{1}{4}$. Le fait, habituel pour nous, d'utiliser les mêmes expressions de nombres quelque soit la grandeur qu'ils désignent est en l'occurrence une exception. Cela n'étant justement pas habituel pour nous, nous ne l'avons pas envisagé. Il vaut la peine de remarquer que nous avons précisément cru comprendre la traduction de la croix quand nous nous trompions dans son interprétation, ne faisant que perpétuer le préjugé consistant à supposer que les expressions des nombres et des fractions sont indépendantes de la nature des grandeurs associées. La satisfaction éprouvée dans notre interprétation de la croix ne saurait être prise pour le gage d'une interprétation correcte. Arriver à donner du sens à une expression, même quand c'est apparemment le bon, ne garantit en rien que notre interprétation soit correcte. C'est une expérience dont il est sans doute utile de se souvenir. Et c'est à l'inverse grâce aux expressions que nous ne comprenions pas que nous avons pu remettre en cause notre préjugé qui n'engage rien moins que notre conception des nombres et qui est par conséquent particulièrement difficile à découvrir et a fortiori à remettre en cause.
Pour s'assurer que le « théorème de Thalès » est utilisé dans ce problème il nous fallait au moins disposer d'une traduction de la figure et des nombres qui y sont inscrits. Ce rapide parcours de la traduction de la figure proposée par Sylvia Couchoud citée dans l'article de Wikipedia nous a permis de découvrir un certain nombre des difficultés et des incertitudes inhérentes à une telle traduction. Et même si ce n'était pas du tout notre propos, cela nous a fait découvrir un important préjugé sur notre conception des nombres dont on a pu ainsi voir le rôle dans notre interprétation. A nouveau, nous avons découvert autre chose que la confirmation que nous cherchions. Cela n'empêche pas que bien d'autres interprétations et traductions soient possibles... En voici rassemblées quelques-unes :
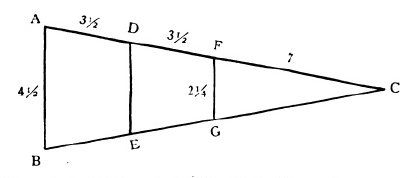
|
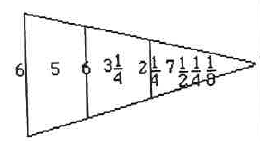
|
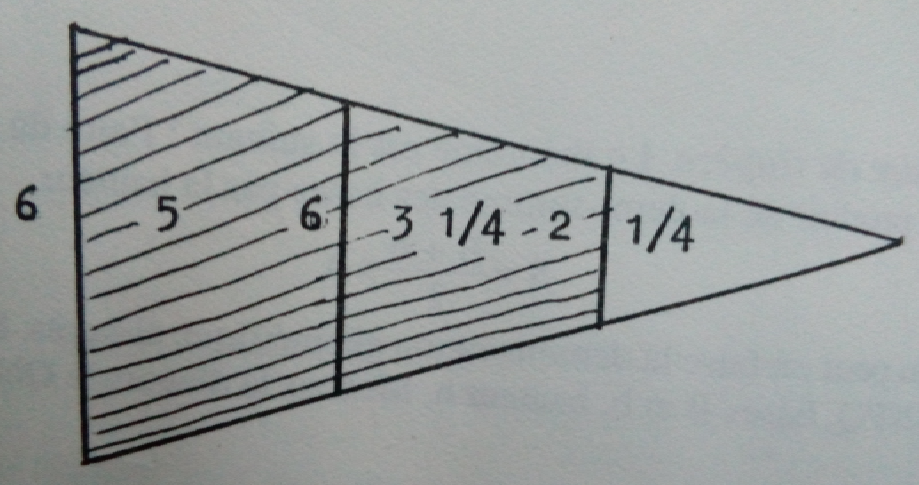
|
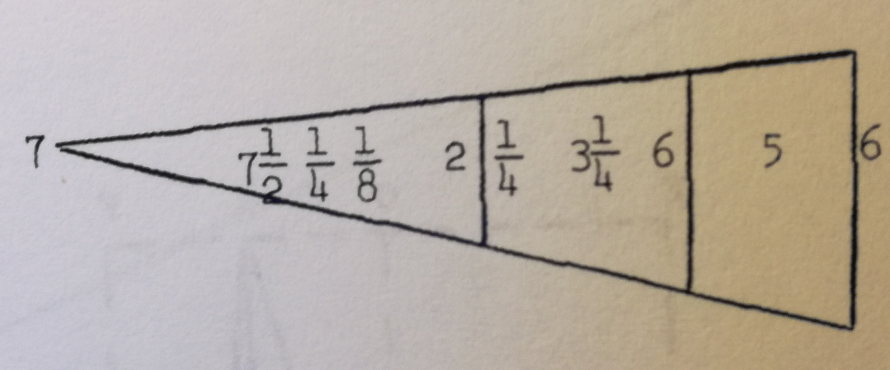
|
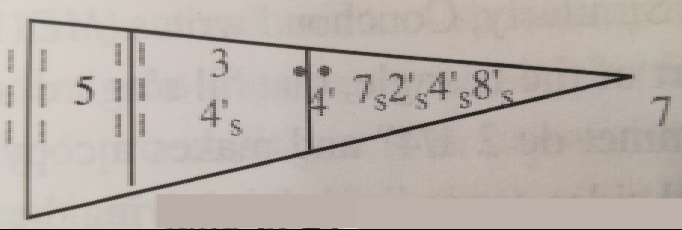
|
|
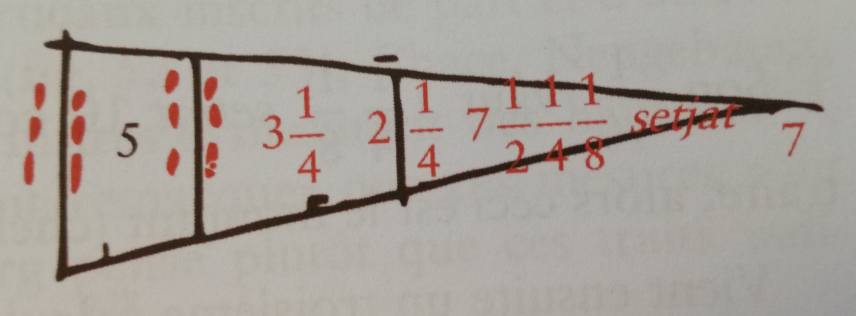
|
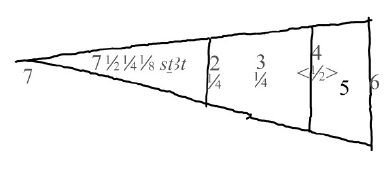
|
Sans analyser et commenter toutes leurs différences, on peut en dégager facilement quelques-unes. Seul Clagett propose la même traduction de la figure que Sylvia Couchoud (en ajoutant le 7 oublié dans la figure de Couchoud). Les traductions de Friberg et de Michel distinguent les nombres correspondant à la mesure d'une surface de ceux d'une longueur. Mais Friberg fait apparaître deux nombres correspondant à des surfaces, et Michel un seul. Pour Friberg et Michel, les six traits qui entourent la base et le premier trait de division ne sont pas l'expression d'un nombre, mais des marques qui indiquent les côtés dont on chercherait à déterminer la longueur. Cela change bien sûr complètement l'interprétation de la figure et celle du problème. Mais Miatello (2015, p. 65) ne retient pas cette interprétation et conteste les arguments donnés pour cela par Michel. Distinguer ce qui est un nombre de ce qui n'en est pas un est aussi sujet à interprétation.
De toutes ces traductions, seule celle de Chace & alii 1927 présente une disposition des nombres et des valeurs permettant de reconnaître une configuration de Thalès. Outre que c’est la seule, il est aussi manifeste que cette figure nous présente plus l'interprétation que ces auteurs font de ce problème qu'une traduction de la figure. Eux seuls aussi interprètent le 7 comme la longueur d'un côté du triangle de pointe, Couchoud, Clagett, Friberg, Michel et Matiello l'interprétant comme la hauteur du plus grand triangle. Sur aucune des autres traductions on ne peut reconnaître la configuration de Thalès que l'encart nous faisait pourtant voir. Reconnaître cette configuration est en particulier exclu pour toutes les interprétations dans lesquelles les six traits qui entourent les deux premières lignes verticales ont été traduits par des 6, rendant égales les deux premières lignes verticales. Voici à présent les figures données par Clagett et Miatello correspondant à leur transcription des valeurs de leur figure :
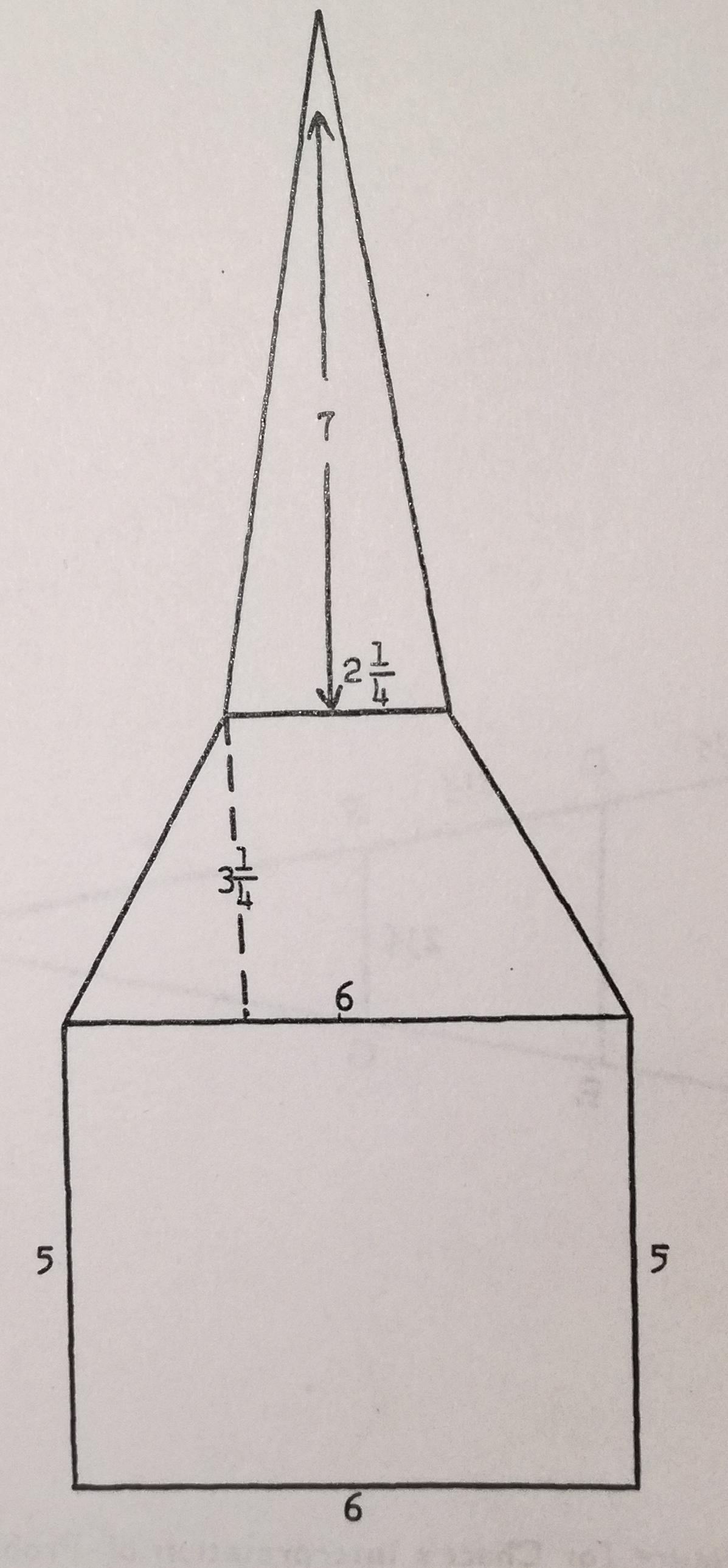
|
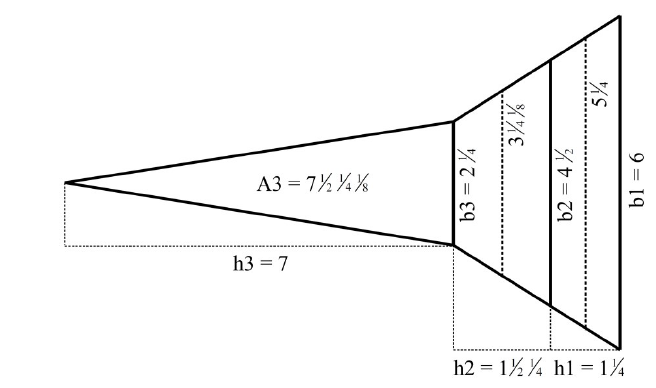
|
| Clagett 1999, p. 383 | Miatello 2015, p. 66 |
Suivant ces interprétations, l'évidence même que la figure soit celle d'un triangle est remise en cause. Il ne saurait plus être question d'y reconnaître le « théorème de Thalès ».
Théophile Obenga affirme lui explicitement que le « théorème de Thalès » est appliqué dans ce problème :

Le problème consiste pourtant selon lui à calculer l'aire du trapèze au milieu du triangle. Or le calcul qu'il en donne (sans se rapporter ni à une transcription ni à une traduction de la procédure) ne fait pas intervenir ce théorème. La disposition et les valeurs qu'il donne des nombres dans sa figure (voir ci-dessus), ne justifient pas non plus cette affirmation. Friberg et Michel supposent dans leur interprétation que la procédure utilise la proportionnalité des côtés dans deux triangles semblables, c'est-à-dire le « théorème de Thalès ». Couchoud, on l'a vu, ne le fait nulle part intervenir et ne le mentionne pas.
Notre propos n'est pas, et ne saurait être, de décider de l'interprétation du problème 53. Il ne s'agit pas non plus de trancher la question de savoir si le « théorème de Thalès » était ou non connu, d'une manière ou d'une autre (ce qui peut faire des différences...), des Égyptiens. Il ne s'agit ici que d'examiner le fonctionnement de l'encart historique qui présente aux élèves et aux enseignants une image du problème 53, pour lesquels seule la figure peut être signifiante, comme une preuve manifeste de l'usage par les Égyptiens du « théorème de Thalès ». Ce rapide examen de la traduction de cette figure auquel nous nous sommes livrés a montré les difficultés et les incertitudes inhérentes à une telle traduction, ainsi que les connaissances qu’elle suppose. Il est tout simplement impossible à partir de ce problème, et a fortiori à partir de sa seule figure, de déterminer la valeur et la signification des nombres de la figure et dès lors d'établir qu'il y aurait là une configuration de Thalès. Les deux spécialistes qui considèrent que ce théorème est utilisé dans ce problème ne se fondent pas pour cela sur la figure, ni même sur le texte de ce problème pour utiliser eux-mêmes ce théorème dans leur interprétation de la figure et du problème. L'encart qui présente l'image du manuscrit comme une preuve manifeste de l'usage du « théorème de Thalès » exploite donc une fausse évidence. Il induit les élèves en erreur et cultive un raisonnement faux : si nous voyons une configuration de Thalès, c'est qu'il y a une configuration de Thalès. Comme surtout nous ne sommes spontanément guère capables d'envisager autre chose qu'une configuration de Thalès, ni enclins à le faire, nous tenons pour établi ce que nous envisageons. Une fois ce raisonnement explicité, personne ne peut y adhérer. C'est bien pourtant celui tenu par tous les encarts, articles, livres, sites qui donnent cette figure à cet effet et par tous ceux qui y ont vu une manifestation de ce théorème. Ne pouvant y voir autre chose qu'une configuration de Thalès, nous y voyons la preuve de sa présence. Cela revient à ne pas envisager, et même à tenir pour entendu, que les choses ne puissent être autrement que nous les concevons. Mais cette présence n'est en l'occurrence qu'un produit de notre interprétation, elle est notre reflet. Une telle lecture est fondamentalement circulaire : nous ne faisons qu'y retrouver ce que nous y avons mis en étant ensuite satisfaits de retrouver ce que nous connaissons. La figure de la configuration de Thalès, les nombres qui y sont portés et le théorème de Thalès sont autant de faux-amis. A l'inverse de l'intention déclarée, l'histoire ainsi pratiquée ne conduit pas tant à une ouverture d'esprit qu'à renforcer notre propre conception en tenant pour entendu que c'est la seule possible, et ce faisant à la reconnaître là où elle n'est pas forcément à l'œuvre. Nous avons déjà vu cela avec le traité de Rouche et Comberousse dans lequel on reconnaissait ce que nous y introduisions nous-mêmes, à savoir l’idée qu’une dénomination comme celle du «théorème de Thalès » permet de faire de l’histoire. Les diverses interprétations données de la figure par différents spécialistes, une seule en l'occurrence aurait suffit, montrent à l'inverse que l'histoire, en revenant aux textes, peut bien au contraire nous donner les moyens d'envisager d'autres interprétations et ce faisant nous soustraire aux effets d'une conception unique. En introduisant quelques-unes de ces interprétations, nous nous sommes avant tout donnés des interprétations alternatives à celle que nous envisagions « spontanément » afin que celle-ci n'apparaisse plus comme allant de soi et ne s'impose plus comme telle. Mais une telle histoire est incompatible avec la concision requise pour un encart.
Les élèves, et les enseignants, sont incités à reconnaître dans la figure du problème 53 du papyrus de Rhind la configuration caractéristique du « théorème de Thalès ». De même, ils sont incités à voir dans le récit de la mesure de la hauteur de la pyramide par Thalès une application du « théorème de Thalès ». Ce théorème n’est pourtant pas nécessaire à la mesure de la pyramide et la configuration qui lui est associée ne se retrouve pas dans la figure du papyrus du Rhind ; il n’est pas même certain que le triangle en soit un ! Nous les y voyons pourtant et nombre d’encarts historiques tiennent pour avéré ce qu’ils montrent et nous font voir. Ils réalisent le tour de magie parfait, celui dont même celui qui le réalise ignore qu’il s’agit d’un tour de magie : leurs auteurs comme leurs lecteurs-spectateurs partagent la même illusion et la reproduisent d’autant plus efficacement qu’ils le font à leur insu. C’est une sorte d’idéal de propagande où chacun colporte d’autant plus volontiers la même histoire qu’il y croit sincèrement. Ce n‘est aussi qu’à la condition de cette adhésion a priori que les encarts peuvent être aussi concis. Car pour être concis ils ont besoin de jouer sur des sous-entendus partagés.
On a vu que de nombreux encarts de nos manuels rapportent le récit de la mesure de la hauteur de la pyramide par Thalès en véhiculant l’idée d’une Égypte arriérée à laquelle le philosophe et mathématiciens grec Thalès vient dispenser son savoir. Cette représentation colonialiste de l’Égypte et de la diffusion du savoir est contredite par les sources grecques qui indiquent une influence inverse. Ainsi, quelques encarts corrigent cette présentation mais sont parfois enclins, comme ceux cités de Magnard et de Didier, à tomber dans l'excès inverse et à attribuer avec des preuves de même nature le « théorème de Thalès » aux Égyptiens. Il n'est pas difficile de trouver des sites faisant encore plus nettement valoir l’antériorité et la prééminence du savoir égyptien. C’est le cas par exemple du site « African Heritage » du Dr Y. (sic) dans lequel la figure du problème 53 du papyrus de Rhind est à nouveau invoquée comme preuve que les Égyptiens connaissaient le théorème de Thalès bien avant les Grecs :
Et sur le même page, on peut lire un peu plus loin une toute autre histoire faisant valoir la supériorité des mathématiques égyptiennes, avec néanmoins toujours le même intérêt pour les dénominations et leurs enjeux :
Un tel texte peut nous aider à mieux apprécier les enjeux et les implications des dénominations adoptées dans nos manuels qui nous présentent une histoire qui n’est pas toujours beaucoup moins caricaturale que celle présentée dans ce site.
Thalès a incarné ici la figure du grand savant ; celui qui a un théorème à son nom et sa place dans les manuels scolaires. Mais l’assimilation de sa notoriété à l’énoncé du « théorème de Thalès » induit inversement l’idée qu’il aurait été célèbre pour avoir découvert ce théorème, c’est-à-dire un théorème aujourd’hui accessible au niveau du collège. Cela peut suggérer que la reconnaissance mathématique s'obtenait alors à bon compte… L’élève peut ainsi rêver à l’impression qu’il produirait s’il avait la possibilité de remonter le temps et de montrer à son tour au Pharaon l’étendue de ses connaissances mathématiques : il serait sans doute encore plus impressionné que par Thalès. Une telle dénomination véhicule ainsi avec elle en même temps qu’elle la conforte une idée du progrès des connaissances qui s’accompagne d’une certaine condescendance à l’égard des mathématiques et des mathématiciens présentés comme les plus grands : en mettant les élèves au niveau de Thalès, elle met aussi Thalès au niveau des élèves. Le bénéfice pédagogique procuré par cette dénomination et ce récit qui en déploie la signification a pour contrepartie l’assimilation des connaissances de Thalès à celles d’un élève de collège.
La condescendance est le fait d’un sentiment de supériorité qui se manifeste dans la possibilité d’attribuer un mérite à celui dont on se sent supérieur. Le mérite accordé, aussi considérable soit-il, est peu de chose comparé au pouvoir manifesté en l’accordant par celui qui l’accorde : en rendant hommage à un mathématicien, j’exerce et manifeste avant tout mon pouvoir de lui rendre hommage, c’est-à-dire d’être en mesure et en position d’en reconnaître la grandeur. Je prends part à sa grandeur et j’y prends une part qui ne lui revient pas ; celle de la lui reconnaître. C’est un jeu auquel on joue en étant assuré d’en rester maître et qu’il nous faut jouer pour exercer notre magister. C'est une forme de politesse excessive de celui qui se sent fort de son sentiment de supériorité et qui ce faisant le met en œuvre et le conforte. C’est typiquement le cas d’un adulte qui traite ostensiblement un enfant en adulte : c'est sans risque pour l’adulte qui a le pouvoir inaliénable de faire croire à l’enfant qu'il le traite en adulte, ne lui accordant que ce qu’il peut lui accorder, mais certainement pas le pouvoir d’être traité par lui de la même manière. L’adulte joue de sa supériorité en la mettant en jeu mais qu’il conforte par le fait même de feindre d’abandonner cette différence. De même, en attribuant à Thalès son théorème, c’est exclusivement notre conception de ce théorème que nous entendons lui reconnaître et c’est nous qui sommes en mesure de reconnaître qu’il l’a introduite. Nous ne lui cédons pas la possibilité de mettre en cause notre conception de ce théorème, mais seulement de la conforter en la lui attribuant.
L’assimilation d’un théorème présenté comme ayant été découvert par Thalès à celui enseigné aux élèves procède aussi d’une certaine conception de l'histoire des mathématiques et la conforte. Cette assimilation n’est propre ni à ce théorème, ni mêmes aux théorèmes ; elle se retrouve dans les définitions, les procédés de calcul etc. enseignés dont les encarts historiques s’attachent à déterminer l’origine. Elle est en fait le ressort d’une représentation très prégnante selon laquelle la progression scolaire de l’élève suivrait à peu près le développement historique des mathématiques. Ainsi, au cours de sa scolarité l’élève devrait parcourir les différents stades par lesquels les mathématiciens seraient eux-mêmes passés. Son cursus récapitulerait le développement des mathématiques. Son développement individuel reproduirait de manière sommaire celle des mathématiques. En quelques années il accomplirait une évolution semblable à celle qui s’est produite sur plusieurs millénaires. Ainsi, il a appris à compter à l’école primaire comme ont dû le faire les scribes les plus éduqués des premières grandes civilisations mésopotamiennes et égyptiennes. Mais l’enseignement des nombres négatifs va vite lui faire dépasser ce stade qui lui apparaîtra aussi de ce fait comme primitif. La question de leur origine en est d’autant plus fascinante qu’avec elle semble se poser inversement celle de notre évidente et irréductible supériorité. L’expérience se renouvellera plus tard avec les nombres complexes. Leur enseignement procède d’une sorte de rite de passage. L’enseignement de la géométrie au collège, et notamment le « théorème de Thalès », fait découvrir à l’élève ce qui peut lui apparaître comme étant le summum de la géométrie grecque. Il poursuivra sa progression tant historique que scolaire en découvrant ce qui pourra lui sembler être les plus remarquables découvertes en algèbre, sur les fonctions, leurs dérivées, le calcul intégrale, etc. Chaque notion enseignée est pour lui simultanément l’acquisition de connaissances nouvelles et le dépassement des mathématiciens qui l’ont ignorée. Les mathématiques qui lui sont enseignées le font repasser par les grandes étapes de l’histoire des mathématiques et en sont en même temps l’aboutissement. Les encarts historiques sont aussi inversement autant d’occasions de mettre en place et de conforter cette récapitulation et ce faisant de donner aux élèves eux-mêmes, et non seulement aux connaissances, une place privilégiée dans cette histoire.
Le principe de la récapitulation de l’histoire par le parcours scolaire a sa déclinaison didactique : c’est l’idée selon laquelle l'histoire des mathématiques permettrait de retrouver les difficultés auxquelles les élèves sont confrontés. Ses difficultés seraient aussi celles que Thalès, Euclide, Archimède, Descartes, Leibniz, Euler, Gauss etc. ont dû surmonter avant eux. Elle fonde ainsi tout un usage didactique de l’histoire. Il est rassurant et même flatteur de penser que les plus grands mathématiciens seraient aussi passés par là. Voir ses propres difficultés chez eux permettrait aussi de mieux les identifier et aiderait à les surmonter : le progrès des mathématiques a transformé la poutre à laquelle ces mathématiciens ont été confrontés en une paille pour les élèves. Cet usage didactique de l'histoire se fonde sur la récapitulation en même temps qu’il la conforte. L’élève rejouerait en classe une scène primitive constitutive de la célébrité d'un mathématicien. Le cadre scolaire ordinaire est ainsi mis en correspondance avec des moments historiques. La classe devient le théâtre où se rejoue l’histoire des mathématiques. Le tableau noir devient le grand écran qui nous fait revivre l’épopée des mathématiques. Craignant qu'il ne s'ennuie dans sa pataugeoire, on dit à l’élève qu’il est en fait au milieu de l’océan en route pour découvrir l'Amérique ! Il y a là bien sûr inversement de la condescendance puisque cela implique que ses difficultés sont les mêmes que celles qui ont fait la notoriété de grands mathématiciens : ils pataugeaient eux-mêmes dans ce qui leur semblait alors être l’océan, les poutres auxquelles ils se croyaient confrontés n’étaient en fait que des pailles. L’exaltation ainsi procurée se paye de condescendance. Il est aussi attendu que l’élève surmontera ces difficultés, qu’il sera Thalès plutôt que de rester un Pharaon ignorant, faisant de lui au minimum l'égal de ces mathématiciens qui surmontèrent les mêmes épreuves et laissant leurs prédécesseurs sur place. Le chapitre ou la classe suivante le fera immanquablement les dépasser, il deviendra Descartes laissant loin derrière lui Thalès qui ne sera plus qu’un souvenir… (voir l’étude consacrée à un encart relatif à la contribution de Descartes) Surmonter ses difficultés devient aussi dépasser les mathématiciens supposés les avoir rencontrées. L’élève ne va pas s’arrêter là ! Sans doute fera-t-il ensuite des études supérieures, laissant aussi sur place cette fois ses enseignants du collège et du lycée ; c’est aussi le risque auquel expose ce rapport à l’histoire et la condescendance qui lui est inhérente.
La dénomination de « théorème de Thalès » suppose l’identification de l’énoncé attribué à Thalès et de l’énoncé actuellement enseigné. Cette identification est aussi nécessaire à l’idée que les élèves repasseraient au cours de leurs études par les grandes étapes de l’histoire des mathématiques. Elle se retrouve encore dans l’idée que leurs difficultés seraient celles rencontrées par les mathématiciens qui les ont précédés. Elle est l’un des principaux ressorts de la représentation de l’histoire des mathématiques à l’œuvre dans les manuels. C’est elle qui permet de réduire la connaissance de la dimension historique des notions enseignées à la position d’un point sur une droite, lui faisant aussi perdre toute épaisseur. Du fait de cette identification, les récits de la mesure de la pyramide apportent une confirmation qui n’est que circulaire de l’attribution de ce théorème à Thalès présupposée par son appellation.
L’examen des sources a permis de se convaincre que la supériorité des Grecs sur les Égyptiens était un trait ajouté tardivement. Tous les témoignages, qu'ils soient relatifs ou non à Thalès, indiquent explicitement que la science grecque s'est au contraire développée à partir de la science égyptienne et que Thalès s’y est rendu en élève plutôt qu’en maître. Elles ont permis d’établir que cette impression de supériorité était un ajout ultérieur sans fondement historique, perpétrée par les manuels plutôt qu'un fait historique établi. Cela aurait pu être avéré, il n'en demeurerait pas moins que le sentiment de supériorité aurait été la corde sur laquelle ils joueraient. Qu'elle ne le soit pas permet de mettre plus facilement en évidence que l'attrait de ce sentiment de supériorité importe plus que la vérité historique. Et s’il y a fait historique, ce n'est pas de l'histoire des mathématiques en Égypte ou en Grèce antique qu'il s'agit, mais bien plutôt de l'histoire des représentations que l'on s'en fait et que l’on en donne actuellement dans les manuels. La condescendance une fois reconnue, il n'est ensuite plus nécessaire de se reporter aux sources pour en repérer les manifestations dans de nombreux encarts dont elle est de fait un des principaux traits récurrents. Les encarts font partie de manuels scolaires. Ils ont été élaborés pour ce cadre et répondent à certains usages attendus. Il est aussi important que difficile de déterminer ce que cela implique sur les interprétations et les usages que nous pouvons en faire. En tant qu'enseignants, nous savons utiliser ces manuels. Les difficultés que peuvent avoir les élèves à « bien utiliser leur livre » ou à « comprendre un énoncé » sont en partie liées aux connaissances plus ou moins tacites que cela implique. Cela comprend bien sûr une maîtrise de la langue, de son vocabulaire et de sa grammaire, mais encore bien plus. Savoir utiliser son manuel, savoir résoudre un exercice, c'est d'abord commencer par comprendre tout un ensemble de présupposés dans les questions et dans les réponses attendues. L'enseignant est en partie là pour les inculquer. La distinction entre défi et énigme s'estompe : ce que l'enseignant propose comme un défi peut apparaît à l’élève comme une énigme... Nous serions sans doute surpris si nous apprenions que quelqu'un tenait les encarts de nos manuels pour des sources historiques sur l'usage du « théorème de Thalès » par Thalès. Nous savons ce que nous pouvons et ne pouvons pas faire avec un manuel. Nous savons que sa finalité pédagogique le rend impropre à certains autres usages. C'est pourtant le risque auquel nous nous exposons en citant sans précautions Pline, Plutarque, Diogène Laërce, Proclus etc. Le bon usage des manuels est indissociable d'un contexte d'enseignement, institutionnel, culturel, etc. Il est possible d’en repérer certaines manifestations et de se demander si tel élément contenu dans un encart est attesté historiquement ou s'il est une adaptation à ce cadre. Le retour aux sources sera nécessaire pour répondre à ces questions, pour déterminer précisément les éléments ajoutés et ceux retranchés, mais ces questions pourront aussi nous guider dans la recherche des sources permettant d’y répondre.
Les sources ont aussi joué un rôle essentiel dans la remise en cause de l'attribution du « théorème de Thalès » à Thalès. Elles nous ont en effet permis de revenir sur l’évidence de cette attribution sous-jacente aux encarts historiques. Mais il est à présent possible sans avoir besoin d'y recourir de se douter que les autres dénominations sont tout aussi conventionnelles, a fortiori celles qui recourent à des noms propres. Elles ne peuvent aller de soi ; ce sont les produits de nombreux facteurs. Si l'histoire est utile, et même nécessaire, pour déterminer dans chaque cas particulier les facteurs effectivement à l’œuvre, elle ne l'est pas pour savoir que leur choix sont toujours des décisions, qui font intervenir des enjeux, d'autant plus importants que la dénomination est plus fortement institutionnalisée.
Les mathématiques peuvent dispenser de percer les murs d'une pyramide pour en mesurer la hauteur, de nager jusqu'à un navire lointain pour en déterminer la distance. Mais ce qui nous sépare des mathématiques égyptiennes, mésopotamiennes, grecques, ou même d'autres bien plus proches dans le temps, n'est pas a priori de nature mathématique. La distance qui nous sépare des mathématiques passées n’est pas telle qu’une homothétie ou l’action d’un groupe nous permettrait de la franchir et de connaître les mathématiques que nous ne connaissons pas à partir de celles que nous connaissons. Rien ne peut nous dispenser de parcourir la distance qui nous en sépare ; c'est le seul moyen de connaître ce qu'elles partagent avec celles que nous connaissons et ce en quoi elles en diffèrent. Mais nous pouvons au moins un peu connaître certains traits récurrents de notre rapport aux mathématiques passées, rapport lui-même historique, pour en identifier et en contrôler quelques-uns des effets. C'est en partie notre propos d'y contribuer, de faire mieux connaître certaines des transformations inhérentes aux manuels scolaires, la circularité, avec ses faux-amis, la condescendance et la récapitulation, pour mieux en connaître et en identifier les effets. Au delà de ces présupposés récurrents, les sources restent le moyen de découvrir et de suspendre ceux qui risquent autrement de passer inaperçus.